Analiza Danych

Przykłady opisane w tej lekcji dostępne są w arkuszu Excela: Analiza Danych.xlsx tylko ich samodzielne przerobienie daje gwarancję zapamiętania tej lekcji.

Przykłady dla wszystkich lekcji szkolenia Excel 2013: ExcelSzkolenie.pl Cwiczenia Excel 2013.zip

Ta lekcja może być obejrzana lub przeczytana poniżej.

Film wygląda najlepiej jeśli będzie odtwarzany w rozdzielczości 720p HD, rozdzielczość można zmienić dopiero po uruchomieniu filmu klikając na ikonie trybika która pojawi się w prawym dolnym rogu poniższego ekranu. Po kilku sekundach od zmiany obraz wyostrzy się.

Aby móc używać narzędzi Analizy Danych należy wybrać: Menu PLIK " Opcje " Karta Dodatki " przycisk Przejdź….

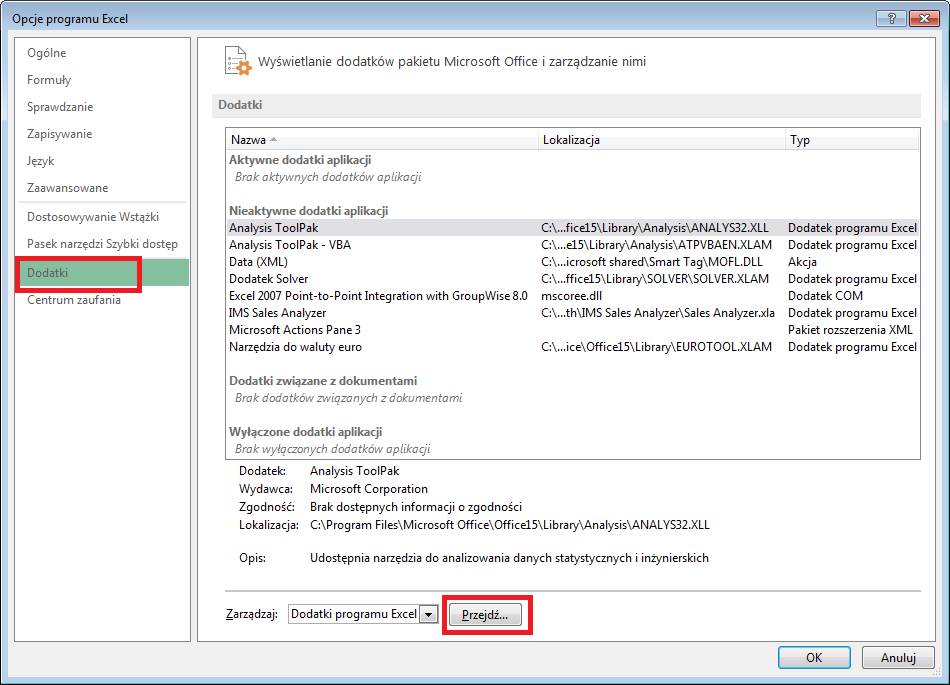
W oknie ‘Dodatki’ wybieramy ‘Analysis ToolPak’ i klikamy OK.

Analiza Danych będzie już dostępna, znajdziemy ją na karcie ‘Dane’.

Przykład 1.

(Arkusz z danymi: ‘Analiza Danych 1’)

(Arkusz z rozwiązaniem: ‘Analiza Danych 2’)

W pewnej firmie zauważono że istnieje duża zależność pomiędzy zmianą ceny a zmianą sprzedaży w sztukach.

Dane po kwartałach dla lat 2005-2009 przedstawione są w poniższej tabeli.

Przygotowano na ich podstawie wykres typu XY, dodano linię trendu i wyliczono funkcję opisującą tą zależność a także współczynnik R².

Postanowiono posłużyć się Regresją aby dowiedzieć się czegoś więcej o tej zależności.

Aby skorzystać ze szczegółowej analizy regresji, należy wybrać polecenie ‘Analiza Danych’ z karty ‘Dane’.

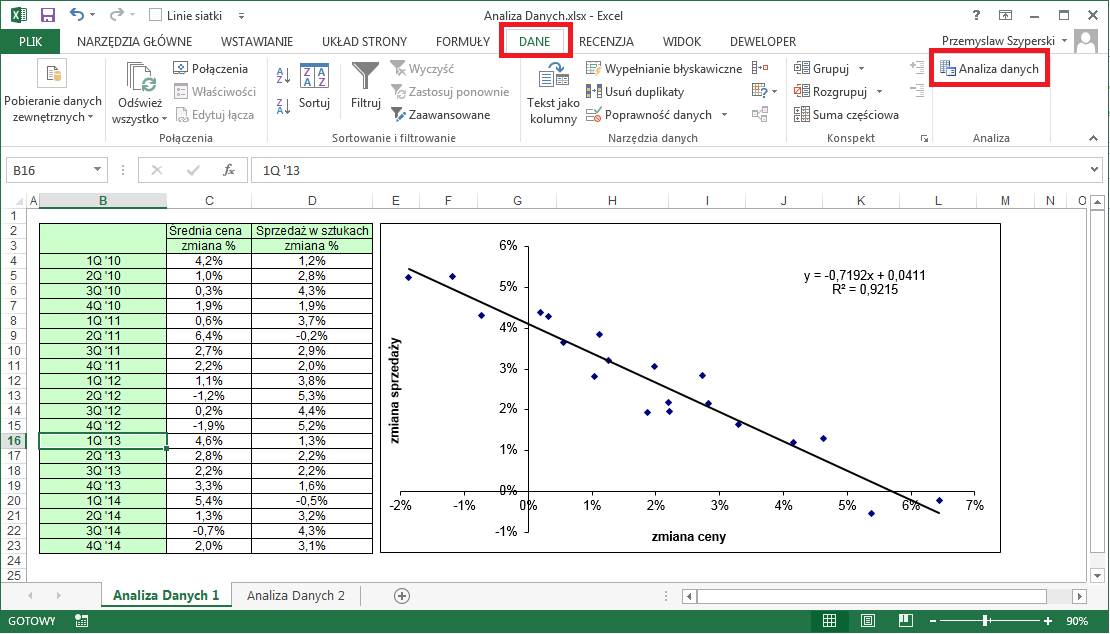
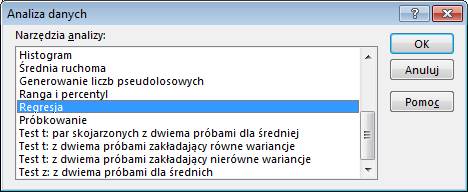
A w oknie ‘Analiza danych’ wybrać ‘Regresja’ i kliknąć OK.

W oknie ‘Regresja’ w okienku ‘Zakres wejściowy Y:’ wprowadzamy dane zmiany sprzedaży w sztukach (ponieważ są one wynikiem zmian cen).

W okienku ‘Zakres wejściowy X’ dane zmian cen (mamy na nie wpływ i to one powodują zmiany sprzedaży).

Zaznaczamy jeszcze ‘Zakres wyjściowy’ i wprowadzamy adres komórki pod tabelą z danymi.

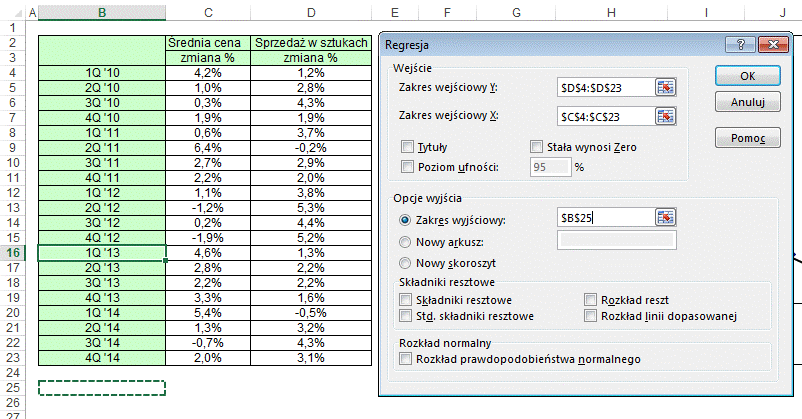
Wyniki Regresji zostaną wprowadzone po kliknięciu OK.

Trzy z nich to dokładniejsze wartości, które mieliśmy już dostępne na wykresie: R kwadrat i współczynniki równania.

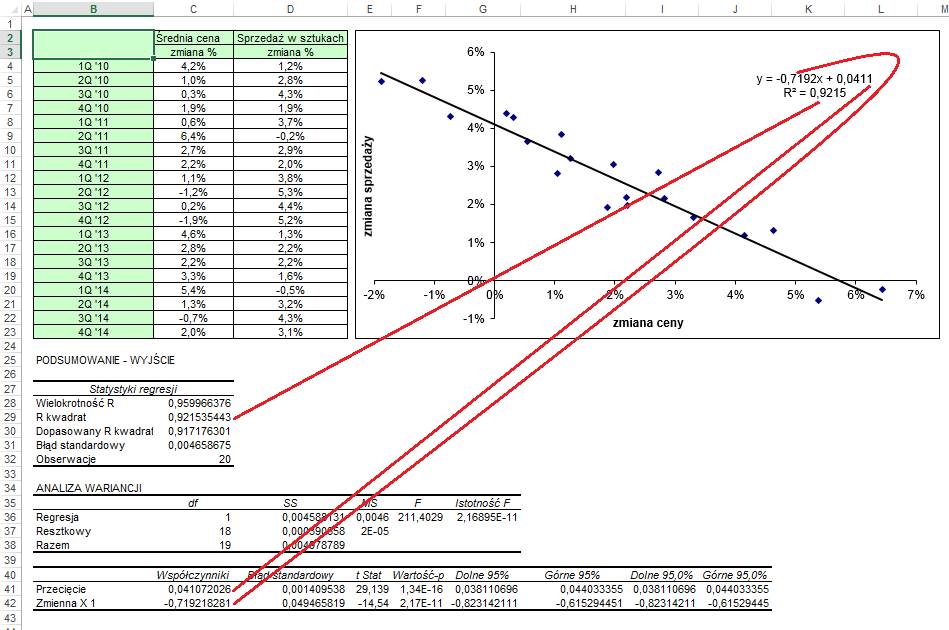
To co nas szczególnie interesuje to ‘Błąd standardowy’.

Dzięki współczynnikom równania będziemy mogli obliczyć zmianę sprzedaży dla zakładanego poziomu zmian cen.

Aby określić jak bardzo rzeczywisty wynik może różnić się od przewidywanego posłużymy się błędem standardowym.

Z prawdopodobieństwem 68% możemy stwierdzić że rzeczywista wartość zmiany sprzedaży będzie znajdować się w przedziale wynik równania +/- błąd standardowy.

Z prawdopodobieństwem 95% możemy stwierdzić że rzeczywista wartość zmiany sprzedaży będzie znajdować się w przedziale wynik równania +/- 2*błąd standardowy.

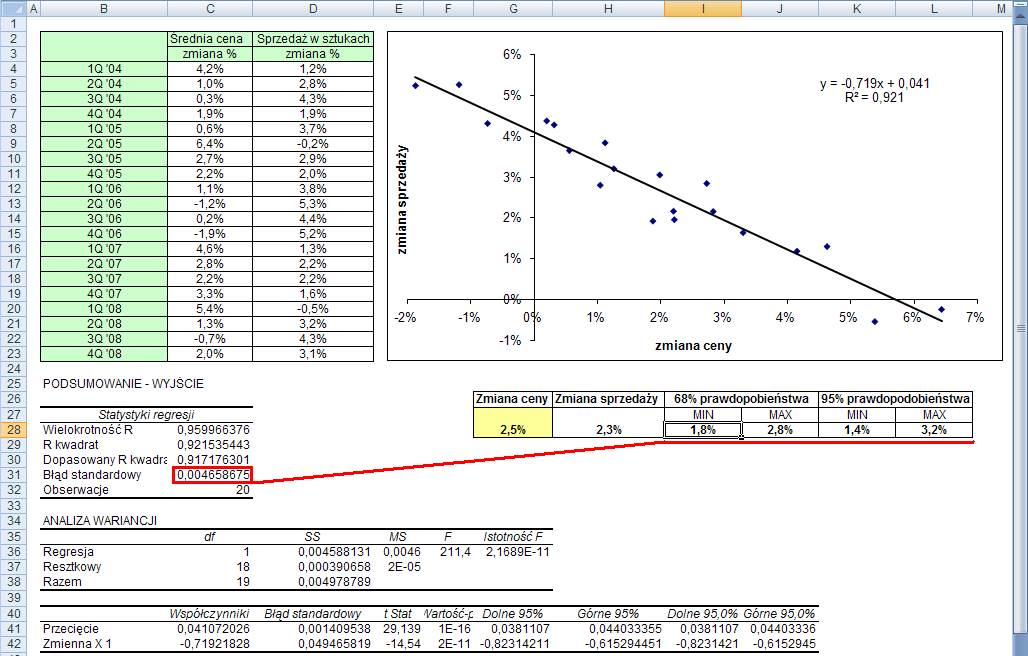
Osoby zainteresowane interpretacją pozostałych wyników odsyłam do podręczników statystyki.

Przykład 2.

(Arkusz z danymi: ‘Analiza Danych 3’)

Histogram to rozkład częstości występowania danego parametru w bandanej próbie. Przedstawiane jest zawsze w podziale na przedziały.

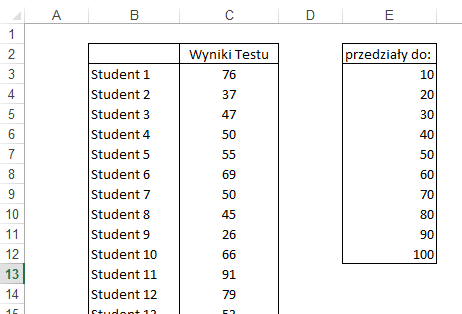
W tym przykładzie 50 studentów pisało test w którym mogli zdobyć maksymalnie 100 punktów. W przypadku braku lub złej odpowiedzi otrzymywali 0 punktów, nie było punktów ujemnych za złe rozwiązanie.

Interesuje nas rozbicie wyników testu w podziale na grupy do 10, 20 itd. co dziesięć.

Wybieramy polecenia ‘Analiza danych’ z karty ‘DANE’.

A następnie ‘Histogram’.

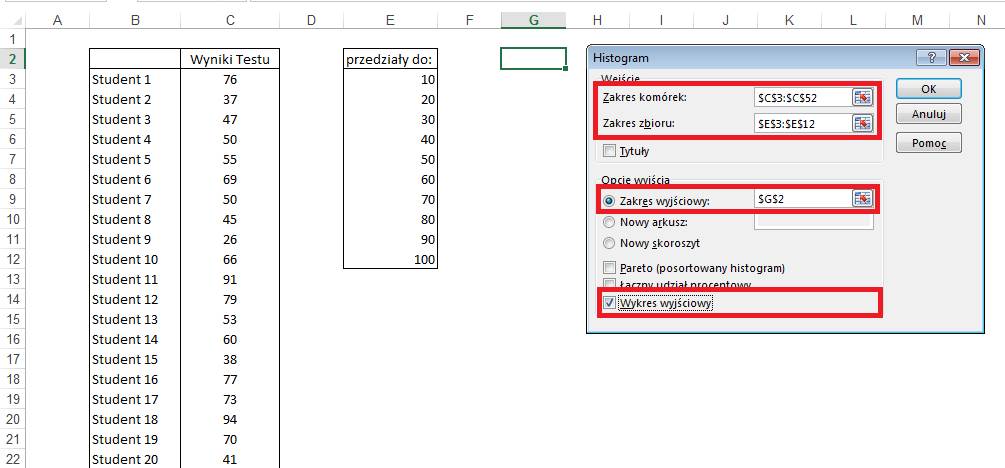
W oknie ‘Histogram’ wskazujemy ‘Zakres komórek:’ czyli wyniki testów, ‘Zakres zbioru:’ czyli na jakie przedziały chcemy ten zbiór podzielić.

Zaznaczamy także aby tabela wynikowa zaczynała się w komórce $G$2, oraz aby oprócz tabeli został dodany także wykres.

Klikamy OK.

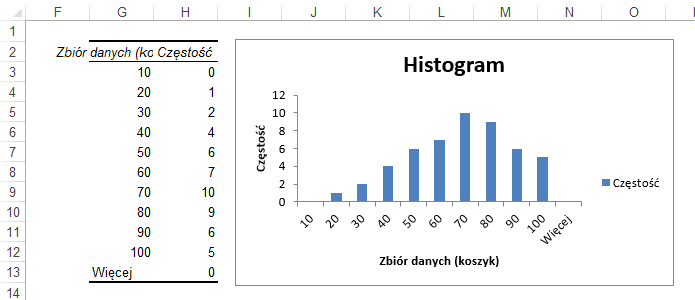
Wynikiem będzie tabela z częstościami i wykres pokazane na poniższym rysunku.

Przykład 3.

(Arkusz z danymi: ‘Analiza Danych 4’)

Generowanie liczb pseudolosowych służy do przygotowywania zbiorów liczb losowych wg założonych parametrów.

W Exelu istnieje funkcja LOS() dzięki której także możemy generować takie liczby, jednak to narzędzie umożliwia wiele opcji niedostępnych dla tej funkcji.

Dokładnie rzecz biorąc generator nie przygotuje liczb losowych a jedynie pseudolosowe, które pod wieloma względami są nieodróżnialne od ciągu uzyskanego z prawdziwie losowego źródła. Dla większość zastosowań takie liczby są w zupełności wystarczające.

Ograniczenie to wynika z faktu, że każdy program wybierający liczby opiera się na pewnych założeniach, które przyjmują skończoną liczbę możliwości i po ich wyczerpaniu wróci do pierwszej.

Wybieramy ‘Analiza danych’ i ‘Generowanie liczb pseudolosowych’.

Następnie wypełniamy pola okna ‘Generowanie liczb pseudolosowych’..

Liczba zmiennych to liczba kolumn które chcemy wypełnić liczbami pseudolosowymi.

Liczba wartości to liczba wierszy które chcemy wypełnić liczbami pseudolosowymi. W tym przypadku wynikiem będzie 1000 liczb (ponieważ 1*1000=1000).

Parametry ‘Pomiędzy’ ‘oraz’ to informacja z jakiego przedziału mają być generowane liczby.

Zakres wyjściowy to lewa górna komórka zakresu w której mają pojawić się liczby pseudolosowe.

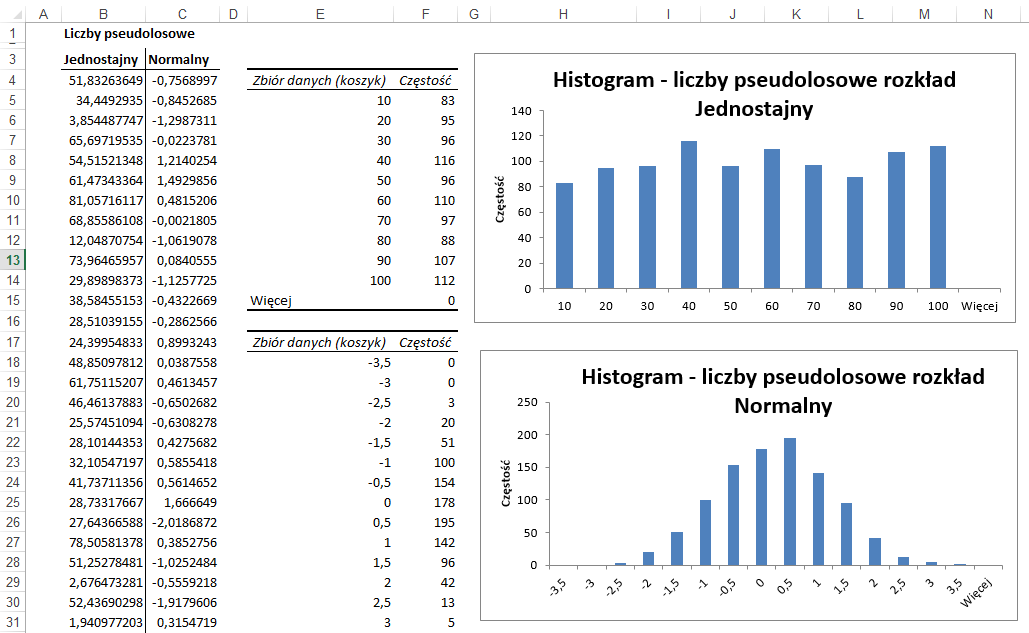
Jeśli chodzi o Rozkład, to gdy wybierzemy tak jak w powyższym przykładzie Jednostajny, liczby będą losowane z takim samym prawdopodobieństwem w każdym z przedziałów od 1 do 1000.

Inną możliwością jest wybranie rozkładu Normalnego w którym liczby są losowane zgodnie z prawdopodobieństwem typowym dla wybranych parametrów rozkładu normalnego.

Rozkład liczb po ich wygenerowaniu można sprawdzić używając opisanego powyżej histogramu.

Inne możliwe rozkłady to:

· Bernoulliego

· Dwumianowy

· Poissona

· Wg wzorca

· Dyskretny

Osoby zainteresowane innymi poleceniami z menu ‘Analiza Danych’ odsyłam do podręczników statystyki, zrozumienie co chcemy obliczyć jest tu o wiele ważniejsze od umiejętności posługiwania się Excelem.