Wykresy Matematyczne

Przykłady opisane w tej lekcji dostępne są w arkuszu Excela: Wykresy Matematyczne.xls, tylko ich samodzielne przerobienie daje gwarancję zapamiętania tej lekcji.

Przykłady dla wszystkich lekcji szkolenia Excel 2003: ExcelSzkolenie.pl Cwiczenia Excel 2003.zip

Przed przystąpieniem do poniższych przykładów należy wcześniej zapoznać się z materiałami w lekcjach: ‘Wykresy Podstawy’ i ‘Wykresy dla Zaawansowanych’, czynności tam wytłumaczone nie są tu ponownie opisywane.

Przykład 1.

(Arkusz: ‘Wielomiany’)

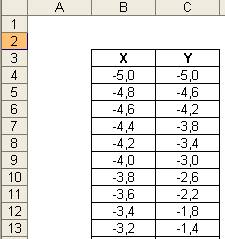
Przygotowanie wykresu funkcji liniowej y=2x+5 zaczniemy od utworzenia tabeli z danymi.

Dla X w pierwszej komórce wpisujemy -5, poniżej -4,8 i przeciągamy te dwie komórki do poniższych aż wartość osiągnie 5.

Dla Y w komórce C4 wpisujemy wzór = 2 * B4 + 5 odpowiadający naszej funkcji i przeciągamy go do poniższych komórek.

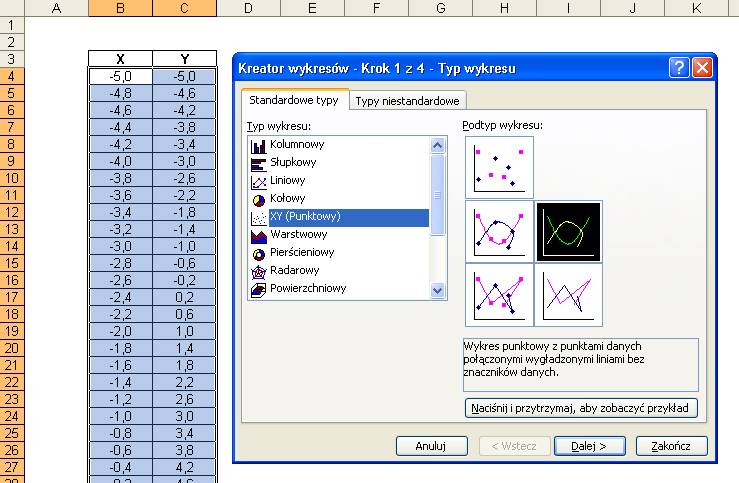
Zaznaczamy całą tabelę z danymi bez nagłówków i wstawiamy wykres typu XY, najwięcej zastosowań ma podtyp zaznaczony poniżej – ‘Wykres punktowy z punktami danych połączonymi wygładzonymi liniami bez znaczników danych.’.

Po wybraniu klikamy od razu przycisk ‘Zakończ’.

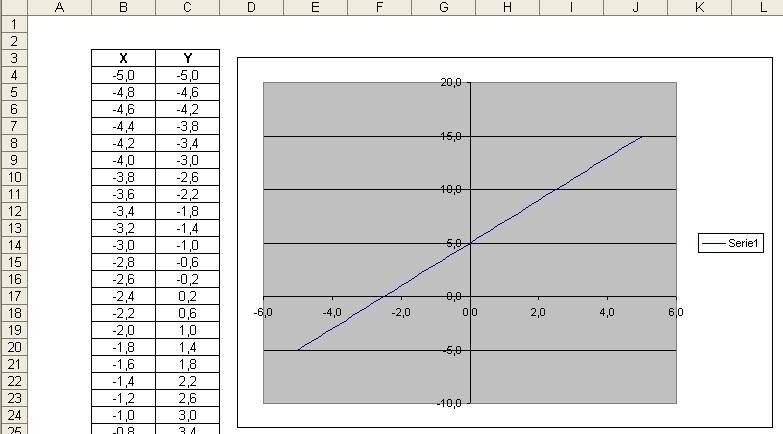
Wstawiony zostanie wykres taki jak poniżej.

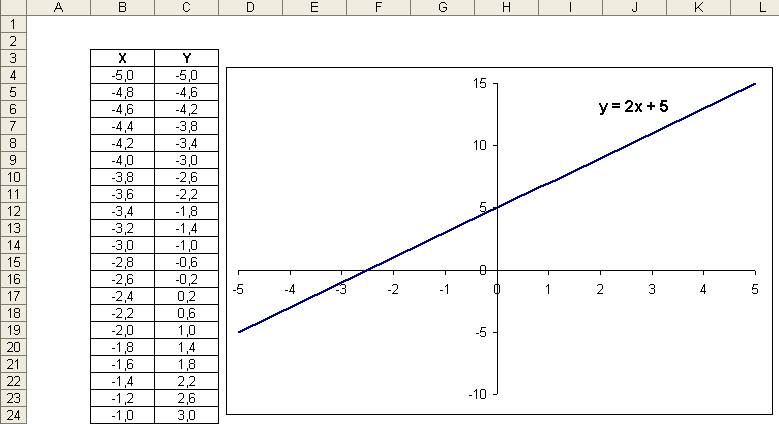
Po sformatowaniu, zmianie zakresu osi i dodaniu tytułu wykresu ze wzorem funkcji uzyskamy poniższy wykres.

W przypadku funkcji liniowej tak naprawdę nie jest konieczne tworzenie tak dużej tabeli danych, wystarczyło by kilka czy nawet dwie, dłuższa tabela potrzebna jest w przypadku wielomianów wyższego stopnia.

Drugim wielomianem jakiego wykres utworzymy będzie y = x³ + x² – 9x -9.

Kroki będą dokładnie takie same, tworzymy tabelę z danymi, wprowadzamy i kopiujemy funkcję.

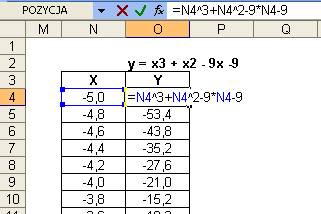
Wstawiamy wykres XY.

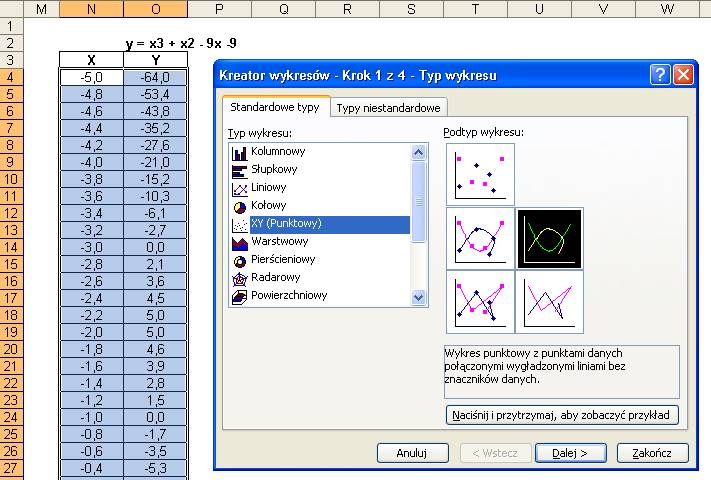
Uzyskamy wykres taki jak poniżej.

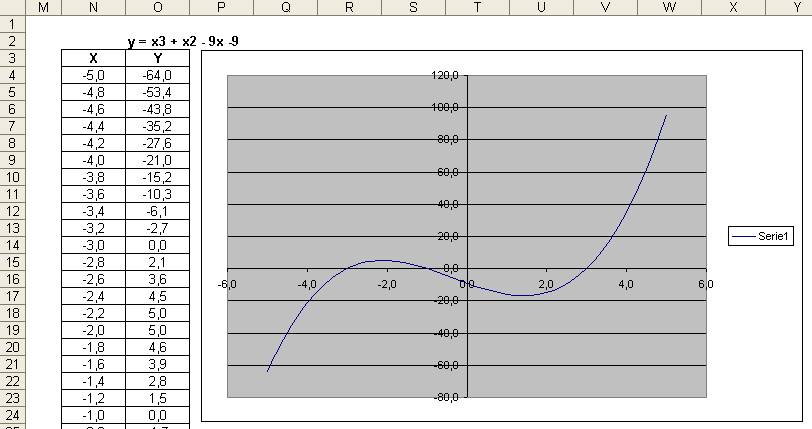
Po sformatowaniu i zmianie max i min osi Y, wyraźnie widać miejsca przecięcia z osią X.

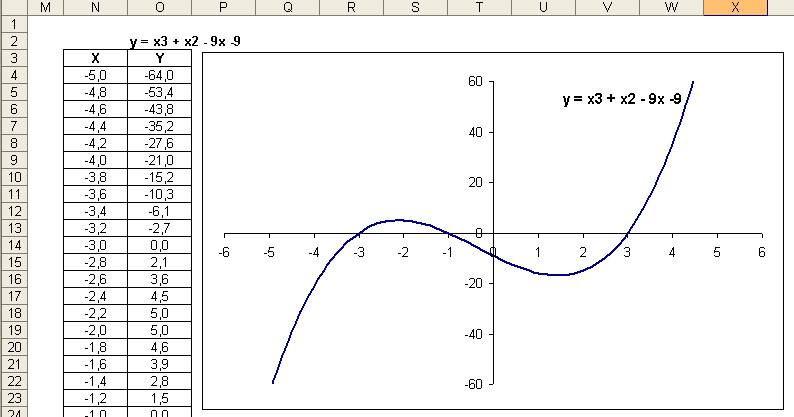
Często zachodzi potrzeba kilkukrotnej zmiany rozpiętości liczb w tabeli danych.

Gdybyśmy zastosowali dla X liczby od -20 do 20, wykres nie wyglądałby tak jak powinien, co widać na rysunku poniżej.

Oczywiście jeśli znamy rozwiązania funkcji trygonometrycznej od razu będziemy mogli wybrać właściwą rozpiętość X.

Przykład 2.

(Arkusz: ‘Funkcje Trygonometryczne’)

Dla większości funkcji trygonometrycznych najwłaściwszą rozpiętością danych jest wielokrotność liczby PI.

Wartość PI możemy uzyskać w Excelu korzystając z funkcji o tej samej nazwie. Po przemnożeniu liczby PI przez liczby od -2 do 2 uzyskamy właściwe wartości X dla funkcji trygonometrycznych.

Poniżej przykłady danych dla funkcji Sinus, Cosinus, Tangens i Arcus Sinus.

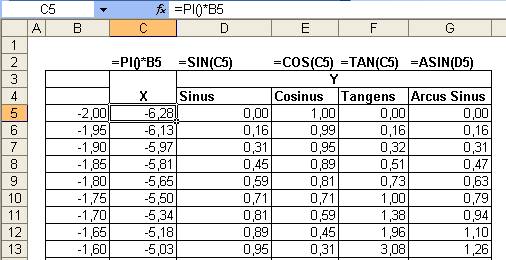
Wykresy Sin i Cos po sformatowaniu i dobraniu właściwych max i min na osiach X i Y.

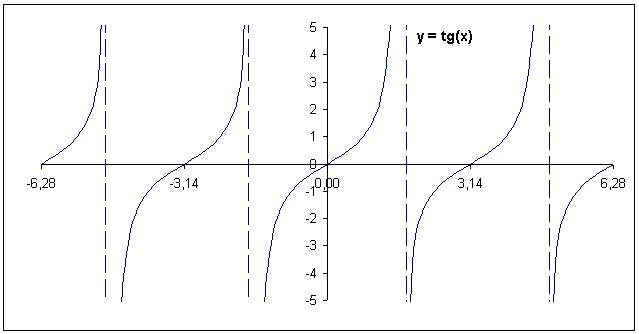
Dla funkcji tangens, możemy sformatować ‘punk danych’ aby skrajne końce były połączone linią przerywaną, co wygląda jak asymptoty, choć w rzeczywistości jest częścią wykresu.

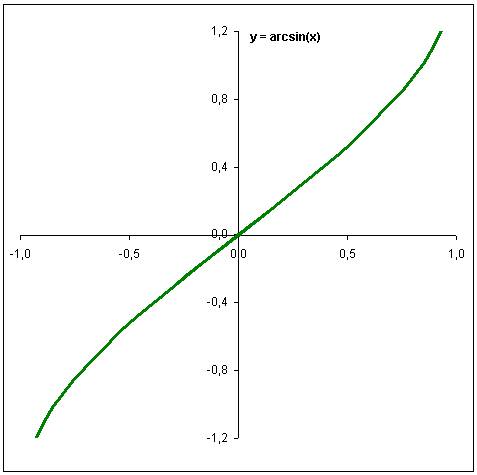
Funkcja Arcus Sinus jako wartości X przyjmuje wyniki funkcji Sinus.

Szkolenie Excel 2003 Szkolenie Excel 2007