Często Używane Wzory
Przykłady opisane w tej lekcji
dostępne są w arkuszu Excela: Często Używane Wzory.xls,
tylko ich samodzielne przerobienie daje gwarancję zapamiętania tej lekcji.
Przykłady dla wszystkich lekcji
szkolenia Excel 2003: ExcelSzkolenie.pl
Cwiczenia Excel 2003.zip
Często sama znajomość Excela okazuje
się niewystarczająca i konieczna jest znajomość podstawowych wzorów
matematycznych.
Wiele razy już przekonałem się nawet
osoba po studiach ekonomicznych postawiona przed problemem obliczenia ceny bez
VAT mając daną cenę z VAT 100zł i VAT 22%, ze zdziwieniem stwierdzała, że nie
jest tego w stanie zrobić.
Poniżej przedstawiam rozwiązanie
problemów z jakimi najczęściej może spotkać się przeciętny pracownik lub
kandydat do pracy na stanowisko gdzie wymagany jest Excel.
Procenty
Wzrost procentowy obliczamy z
następującego wzoru:
Wzrost % = wartość nowa / wartość stara - 1
Wzór ten zastosowano w poniższym
przykładzie do obliczenia wzrostu który wynosi 25%.

Ten sam wzór można także zapisać w
poniższej postaci:
Wzrost % = (wartość nowa – wartość stara) / wartość stara
Czasami bywa że procentowa zmiana z
roku na rok bywa obliczana „od drugiej strony”, w poniższym przykładzie możemy
powiedzieć, że sprzedaż w 2006 roku była o 20% mniejsza niż w 2007. Odbiorcy
takiego komunikatu nie zastanawiając się długo zapamiętują, że różnica wynosi
20%, gdy tak naprawdę jak to obliczyliśmy w przykładzie 1 wynosi ona 25%.
Jest to z reguły celowe wprowadzanie
w błąd odbiorcy i nie zalecam takiego podejścia, no chyba że ktoś zajmuje się
polityką i musi przyjąć obowiązujące w tej branży normy.

Aby obliczyć udział procentowy np.
danego produktu w całości sprzedaży dzielimy sprzedaż tego produktu przez
całość sprzedaży.
Udział procentowy = sprzedaż A / całkowita sprzedaż

Do zwiększenia danej wartości o
procent np. zwiększenie ceny o 22% podatku VAT służy poniższy wzór:
Nowa wartość = Stara wartość * (1 + procent zmiany)

Analogicznie wygląda zmniejszanie o
dany procent, z tą różnicą że zamiast znaku plus jest minus:
Nowa wartość = Stara wartość * (1 - procent zmiany)

Czasami procent o który mamy coś
zmniejszyć podawany jest z minusem (zmniejsz o -20%), co teoretycznie jest
błędem ale niestety jest popularne i należy to rozumieć jako zmniejszenie o
20%. W takim przypadku używamy takiego samego wzoru jak przy zwiększaniu o
procent (minus już jest przy %).
Nowa wartość = Stara wartość * (1 + procent zmiany)

Zupełnie czym innym jest
zmniejszenie o procent a czy innym ‘cofnięcie’ procentu, który został dodany.
W poniższym przypadku z ceny
zawierającej VAT wynoszący 22% chcielibyśmy obliczyć cenę bez VATu.
Użyjemy poniższego wzoru. Do
dodawania określonego procentu mnożyliśmy przez 1+procent, do cofnięcia tej
operacji podzielimy przez 1+procent (działaniem odwrotnym do mnożenia jest
dzielenie).
Wartość bez VAT = Wartość z VAT / (1 + procent zmiany)

Jak widać w powyższym przykładzie
udało się uzyskać oryginalną wartość ceny bez VAT.
Wiele osób zapewne zastanawia się
dlaczego działaniem odwrotnym do zwiększenia o jakiś procent nie jest
zmniejszenie o ten sam procent.
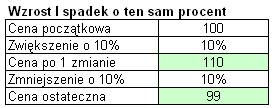
Prześledźmy poniższy przykład w
którym cena została zmieniona dwukrotnie.
Cena początkowa wynosiła 100zł,
została ona powiększona o 10% i po tej zmianie wynosiła 110 (10% ze 100 to 10,
10+100=110).
Cena po 1 zmianie została obniżona o
10% i ostatecznie wyniosła 99zł (10% z 110 to 11. 110 -11 to 99).
Jak widać cena nie wróciła do swojej
oryginalnej wielkości. Im procent zmiany byłby większy tym większa byłaby także
różnica pomiędzy ceną końcową i początkową.
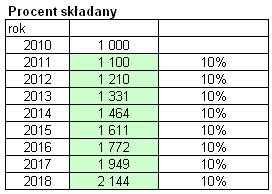
W poniższym przykładzie wartość pewnej
inwestycji wzrasta o 10% co roku, chcielibyśmy obliczyć po ilu latach wartość
ta podwoi się.
W pierwsze z zielonych pól
wprowadzamy wzór na wzrost o procent i przeciągamy go do poniższych komórek. Na
podwojenie się tej kwoty wcale nie musimy oczekiwać aż dziesięciu lat. Kwota
będzie już prawie dwa razy większa w 7 roku a w 8 znacznie przekroczy swoją
dwukrotność. Dzieje się tak ponieważ procent w 2 i każdym kolejnym roku
inwestycji obliczany jest nie od pierwotnej kwoty ale od kwoty już zwiększonej.
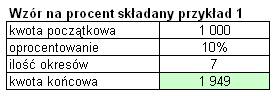
Taki sam wynik możemy uzyskać
znacznie szybciej posługując się wzorem na procent składany:
Kwota końcowa = kwota początkowa * (1 + oprocentowanie) ^ ilość okresów
(symbol ^ oznacza potęgę)
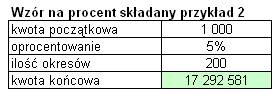
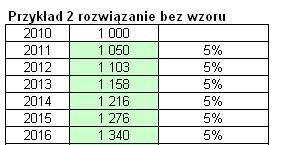
W kolejnym przykładzie na procent składany
pewna osoba zastanawia się czy gdyby dziś wpłaciła 1000 zł na lokatę o stałym
oprocentowaniu 5% i corocznej kapitalizacji odsetek, czy dzięki temu po 200
latach pra pra pra prawnukowie tej osoby byliby milionerami.
Po zastosowaniu powyżej opisanego
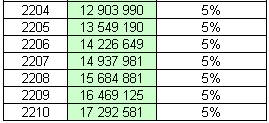
wzoru do takich danych na powyższe pytanie uzyskujemy odpowiedź twierdzącą. Na
koncie po 200 latach pojawi się kwota ponad 17 milionów złotych.
Jeżeli zdecydujemy się na obliczenie
tego samego zadania korzystając z 200 wzorów na wzrost o procent zauważamy że
przyrosty w końcowym etapie lokaty są nieporównywalnie większe od tym z okresów
początkowych, w ciągu kilku ostatnich lat wartość lokaty wzrastała co roku o
ponad milion zł.
…
… …
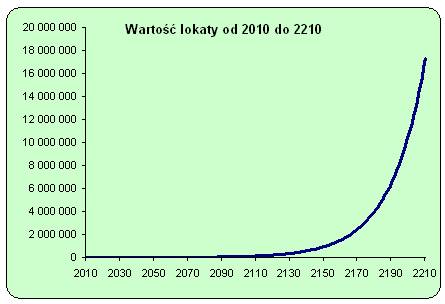
Takie zachowanie się wartości w kolejnych
okresach jest typowe dla funkcji wykładniczych - takich w których zmienna w tym
przypadku ilość lat znajduje się w potędze.
Czy zatem wszyscy powinniśmy
pospieszyć do banków z zamiarem założenia takich lokat? Gdybyśmy chcieli
potraktować te obliczenia nie jako ciekawostkę ale na poważnie należałoby
uwzględnić jeszcze inflację, ryzyko bankructwa banku, ryzyko dewaluacji waluty
lokaty, czy nawet zmiany ustroju, nacjonalizacji lokat bankowych, bankructwa
państwa lub wojny. Po uwzględnieniu tych czynników bardziej rozsądnym sposobem
zainwestowania 1000zł wydaje się przeznaczenie go na podwyższenie swoich
kwalifikacji zawodowych, np. naukę Excela i VBA ;-).
Marża
Obliczanie marży dla wielu osób
stanowi duży problem ponieważ myślą o dodawaniu marży jak o dodawaniu procentu
do danej kwoty.
W rzeczywistości marża nie jest
procentem ‘narzutu’ na koszt, ale stanowi procent jakim jest zysk w ostatecznej
cenie produktu bądź usługi.
Mając dany koszt i procent marży,
cenę obliczamy z następującego wzoru:
Cena = koszt / (1- marża %)
Marża musi być mniejsza niż 100%
ponieważ nie można sprzedając coś zarabiać na tym 100% lub więcej, z każdą
działalnością gospodarczą związane są jakieś koszty.
Marża może natomiast być ujemna,
firma wtedy sprzedaje swoje towary bądź usługi poniżej swoich kosztów i traci
na każdej transakcji.
Wbrew temu co mogłoby się wydawać
wcale nie jest to rzadkie zjawisko, w niektórych branżach np. przy sprzedaży
drukarek, normą jest sprzedaż ich poniżej kosztów, ich producenci pokrywają te
straty z nawiązką sprzedając usługi serwisowe i tonery/tusze z wysoką marżą.
Strategia taka służy w uproszczeniu ‘złapaniu klientów’.

Aby obliczyć marżę znając koszt i
cenę posłużymy się poniższym wzorem:
Marża % = (cena – koszt) / cena
Powyższy wzór możemy także zapisać
jako: Marża % = 1 – koszt / cena

Natomiast jeżeli brakującym
elementem jest koszt użyjemy poniższego wzoru, to ten sam jakiego używamy do
obniżania danej kwoty o procent. Innymi słowy obniżamy cenę o wielkość marży i
pozostaje nam koszt.
Cena = koszt * (1 – marża)

Marża średnia ważona sprzedażą
Do obliczenia średniej marży nie
możemy posłużyć się zwykłą średnią, musimy obliczyć ją korzystając ze średniej
ważonej, gdzie wagami są wielkości sprzedaży.
Możemy to zrobić na 3 sposoby.
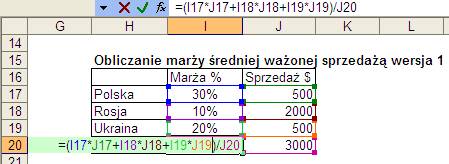
W pierwszym ze wzorów mnożymy każdą
z marż procentowych przez odpowiadającą jej sprzedaż, wyniki sumujemy i sumę
dzielimy przez sumę sprzedaży.
Ten wzór daje nam pełną kontrolę nad
sposobem obliczania i powala zrozumieć na czy polega średnia ważona.
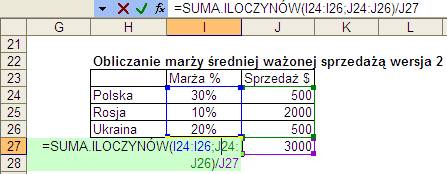
W drugim ze wzorów posłużymy się
funkcją SUMA.ILOCZYNÓW, która sumuje i mnoży marże i sprzedaże, jej wynik
musimy jeszcze podzielić przez sumę sprzedaży.
Funkcja ta jest dokładnie opisana w
lekcji Funkcje.
Trzeci sposób jest dla wielu
najprostszy ale wymaga utworzenia dodatkowej kolumny z marżą kwotową. Wartości
w kolumnie K uzyskujemy dzięki pomnożeniu każdej z marż procentowych przez
sprzedaż.
Aby obliczyć średnią marżę % wystarczy
podzielić sumę marży przez sumę sprzedaży.

Sugeruję wykasować zawartość
wszystkich zielonych pól w arkuszu ćwiczeń do tej lekcji i wprowadzić wzory bez
zaglądania do powyższego opisu. Jeżeli uda Ci się wprowadzić je wszystkie
poprawnie opanowałeś ten materiał, jeżeli nie zawsze można zacząć od nowa i tak
aż do skutku.