Formuły i Funkcje Tablicowe

Przykłady opisane w tej lekcji dostępne są w arkuszu Excela: Funkcje Tablicowe.xlsx tylko ich samodzielne przerobienie daje gwarancję zapamiętania tej lekcji

Przykłady dla wszystkich lekcji szkolenia Excel 2013: ExcelSzkolenie.pl Cwiczenia Excel 2013.zip

Ta lekcja może być obejrzana lub przeczytana poniżej. Opisanych zostało więcej przykładów niż jest na filmie.

Film wygląda najlepiej jeśli będzie odtwarzany w rozdzielczości 720p HD, rozdzielczość można zmienić dopiero po uruchomieniu filmu klikając na ikonie trybika która pojawi się w prawym dolnym rogu poniższego ekranu. Po kilku sekundach od zmiany obraz wyostrzy się.

O formułach tablicowych można by napisać książkę i nie byłaby to broszurka. Ta lekcja ograniczy się tylko do kilku prostych przykładów, osoby zainteresowane tematem i posiadające wysokie zdolności analityczne, z pewnością będą mogły tworzyć znacznie bardziej użyteczne i ciekawe funkcje tego typu.

Niektórzy znawcy Excela twierdzą, że umiejętność posługiwania się Funkcjami / Formułami Tablicowymi jest dobrym wyznacznikiem tego czy ktoś biegle porusza się w Excelu czy też nie, dlatego zdarza się, że funkcje tablicowe pojawiają się na testach dla kandydatów do pracy.

Przykład 1.

Funkcja TRANSPONUJ

(Arkusz: ‘Funkcje Tablicowe 1’)

Funkcja TRANSPONUJ jest chyba najprostszym przykładem Funkcji Tablicowej.

W tym przykładzie chcielibyśmy dane sprzedaży ustawione pionowo pokazać poziomo tworząc łącza do pionowej tabeli.

Zaznaczamy obszar F3:H3, w którym ma znaleźć się tablica wynikowa.

Wprowadzanie funkcji tablicowej zawsze rozpoczynamy od naciśnięcia przycisku F2.

Wpisujemy znak równa się i początek funkcji – wystarczy tr.

Wybieramy podwójnym kliknięciem lewego klawisza myszy zasugerowaną nam funkcję TRANSPONUJ.

 Zaznaczamy obszar tabeli która ma być transponowana. Nie musimy dopisywać zamknięcia nawiasu, tylko od razu kończymy wybierając Ctrl+Shift+Enter.

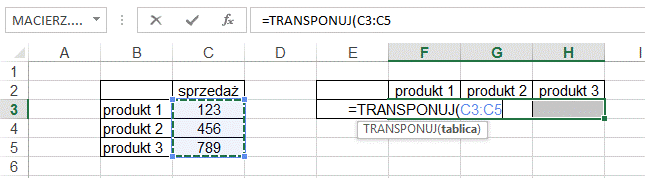
Po wprowadzeniu funkcji tablicowej zawsze kończymy wprowadzanie funkcji wciśnięciem Ctrl+Shift+Enter.

Nie wprowadzamy z klawiatury symboli nawiasów klamrowych, Excel sam je dopisze po wciśnięciu Ctrl+Shift+Enter.

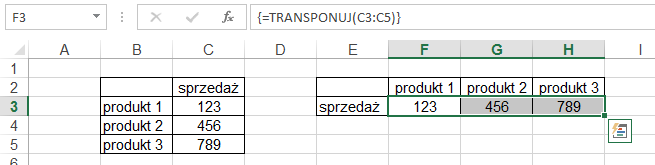
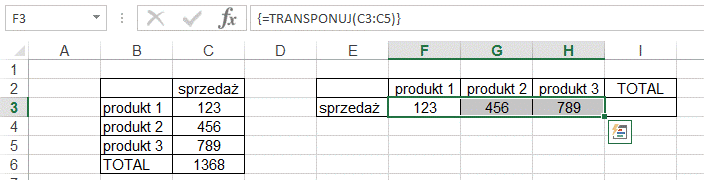
W efekcie powyższych działań w komórkach F3:H3 mamy funkcję tablicową zapisaną w nawiasie klamrowym { }.

Pomimo tego, że funkcja ‘wygląda jakby byla wprowadzona w 3 komórkach jest to jedna funkcja i wprowadzenie zmian w którejkolwiek komórce powoduje zmiany we wszystkich komórkach.

Zmiany wprowadzamy także rozpoczynając od wciśnięcia F2, a po ich wprowadzeniu akceptujemy je wciskając Ctrl+Shift+Enter.

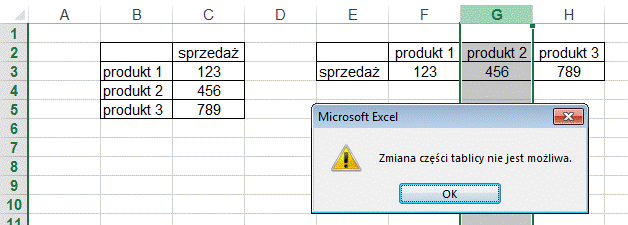
W przypadku tablic zmiana części tablicy nie jest możliwa, np. w powyższym przykładzie nie będzie możliwe dodanie kolumny pomiędzy ‘F’ i ‘G’.

Nie będzie także możliwe wprowadzenie jakichkolwiek zmian inaczej niż poprzez rozpoczęcie wciskając F2 i zakończenie przez Ctrl+Shift+Enter.

W wypadku wszystkich takich prób wyświetlony zostanie poniższy komunikat.

Funkcję tablicową najprościej skasować poprzez zaznaczenie całego zakresu w którym się znajduje i wciśnięcie klawisza ‘Del’.

Zmiana zakresu funkcji lub formuły tablicowej umieszczonej w wielu komórkach jest nieco utrudniona.

Gdybyśmy w tym przykładzie chcieli zwiększyć zakres formuły aby dotyczyła jeszcze komórki C6, należy:

1. Zaznaczyć cały NOWY zakres w którym ma być umieszczona funkcja/formuła po zmianie.

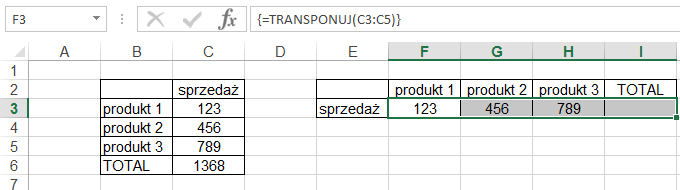
2. Wejść w tryb modyfikacji funkcji tablicowej wciskając F2, następnie zmienić zakres źródłowy na C3:C6 np. przeciągając za róg.

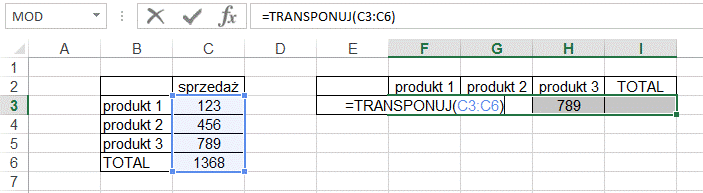
3. Zaakceptować nową wersję poprzez Ctrl+Shift+Enter.

Nie da się tej samej metody zastosować do zmniejszenia zakresu ponieważ musielibyśmy wybrać tylko część tablicy a zmiana części tablicy nie jest możliwa.

W takim wypadku sugeruję:

1. Skopiować formułę jako tekst z pierwszej z komórek, a następnie skasować ją ze wszystkich.

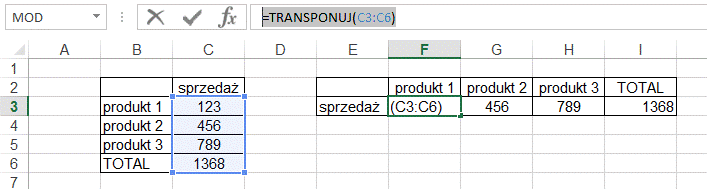
2. Zaznaczyć nowy zakres i w pasku formuły wkleić skopiowaną formułę.

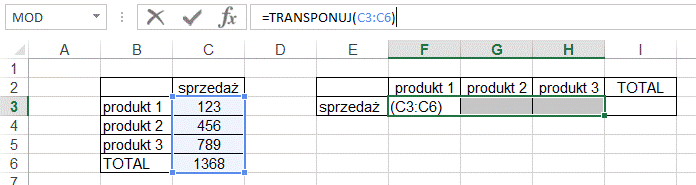
3. Zmienić jej zakres wejściowy np. przeciągając za róg zakresu. Potwierdzić wciskając Crtl+Shift+Enter.

Przykład 2.

Funkcje SUMA i JEŻELI wykorzystane jako funkcje tablicowe

(Arkusz: ‘Funkcje Tablicowe 2’)

Większość ‘zwykłych’ funkcji może być wykorzystana jako funkcje tablicowe. 

W tym przykładzie chcielibyśmy zsumować wydatki dla ‘Kategorii 3’ w Polsce i Rosji.

Funkcje SUMA oraz funkcja JEŻELI mogą być wykorzystana do utworzenia naszego własnego odpowiednika funkcji SUMA.JEŻELI, która będzie sumowała dane z wielu kolumn, czego funkcja SUMA.JEŻELI nie potrafi.

W poniższym przykładzie sumujemy wiele wyników funkcji: JEŻELI, które przyjmują wartości 0 jeśli Kategoria jest inna niż ‘Kategoria 3’ lub wartość wydatków jeśli jest jej równa.

{=SUMA(JEŻELI($B$4:$B$14=$H$4;$D$4:$E$14;0))}

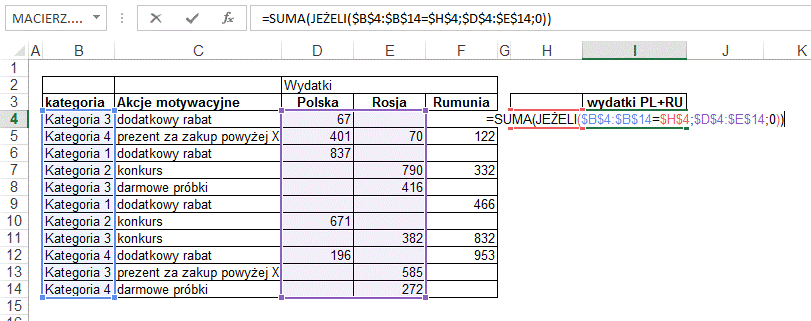
Mówiąc bardziej obrazowo, funkcja JEŻELI zostanie uruchomiona 22 razy - ponieważ tyle komórek znajduje się w zakresie D4:E14, zwróci wartości wydatków dla ‘Kategorii 3’ lub zera, wszystkie te wartości zostaną zsumowane przez funkcję SUMA. 

Przykład 3.

(Arkusz: ‘Funkcje Tablicowe 3’)

W przykładzie 2 połączyliśmy funkcję jeżeli z funkcją suma. Na tej samej zasadzie możemy łączyć funkcję jeżeli z wieloma innymi funkcjami.

Poniżej pokazuję jak możemy utworzyć funkcję tablicową wyszukującą minimum dla produktów z Kategorii 1.

Dzięki odpowiedniemu adresowaniu funkcję tą można skopiować na poniższe komórki i znaleźć minimum dla każdej z kategorii.

Po napisaniu funkcji raz nie będziemy oczywiście tworzyć jej od nowa dla średniej i maksimum, szybciej będzie ją skopiować i użyć polecenia zamień (Ctrl+H) zamieniając MIN odpowiednio na ŚREDNIA i MAX.

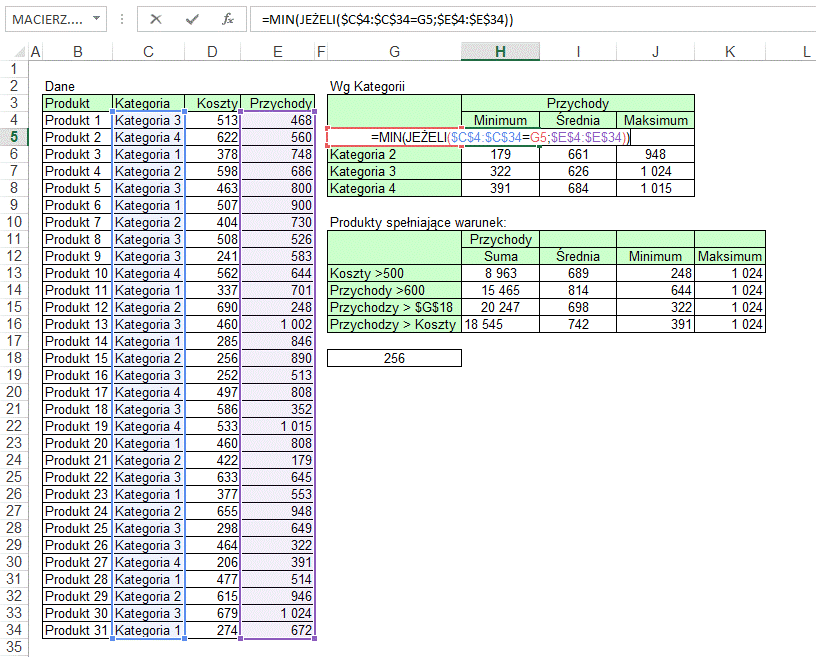
W drugiej tabeli sumuję przychody dla produktów, których koszty są powyżej 500.

Podobnie jak powyżej warunek jest w innej kolumnie (Koszty) niż kolumna sumowana (Przychody).

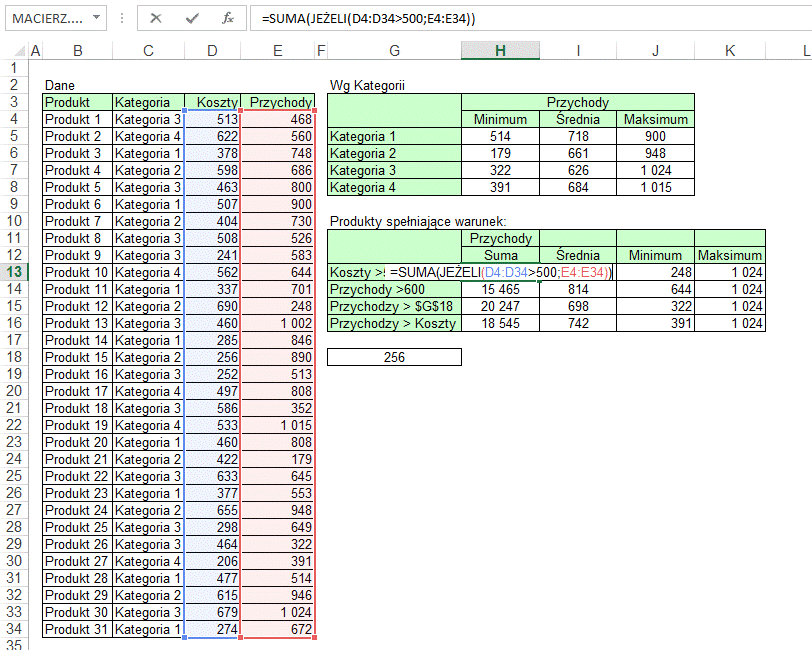
Ale warunek może też być w tej samej tabeli. Poniżej przedstawiona formuła sumuje przychody tylko dla produktów, których przychody przekraczają 600.

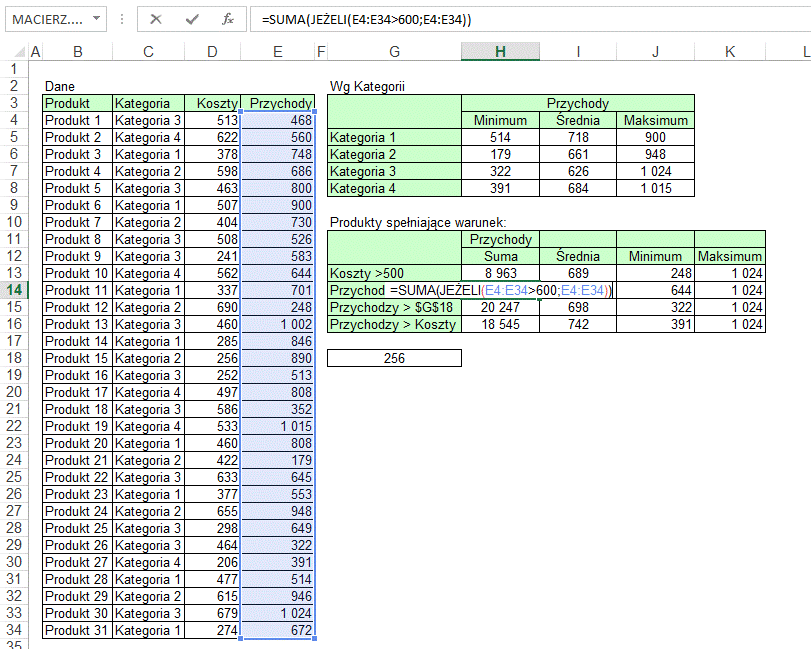
W tym przykładzie kwota przychodów nie jest wpisana w formule ale znajduje się w innej komórce której adres podajemy w formule.

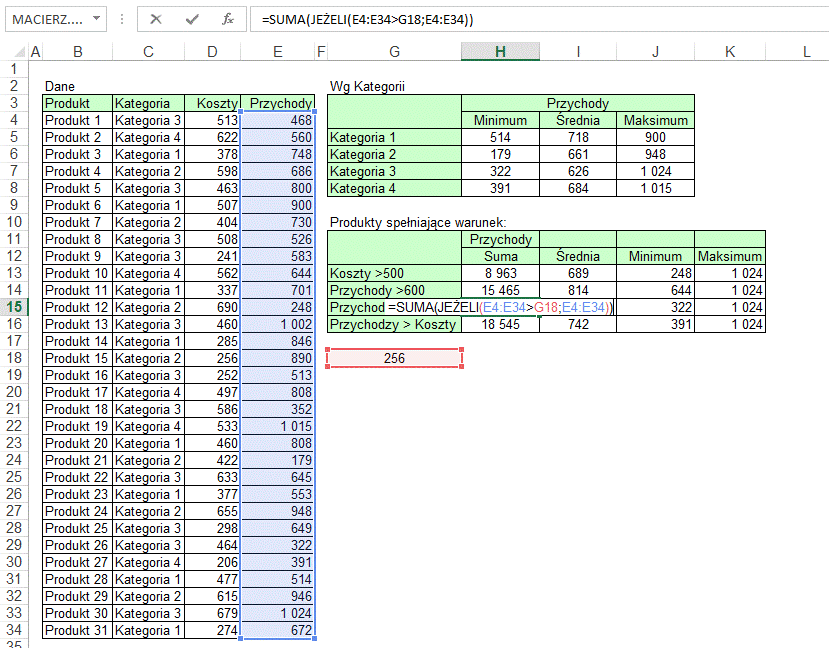
Wreszcie w ostatnim przykładzie warunkiem jest wynik porównania tablic. Sumowane są przychody tylko dla produktów, dla których przychody przewyższają koszty.

Jak widać więc możliwości jest bardzo wiele, jeżeli porównujemy tablicę z pojedynczą liczbą lub adresem, każdy element tablicy będzie z tą liczbą / adresem porównywany. Jeżeli porównamy 2 tablice oczywiście muszą mieć one tyle samo elementów i każdy z elementów jest porównywany z odpowiednim (będącym w tej samej kolejności) elementem 2 tablicy.

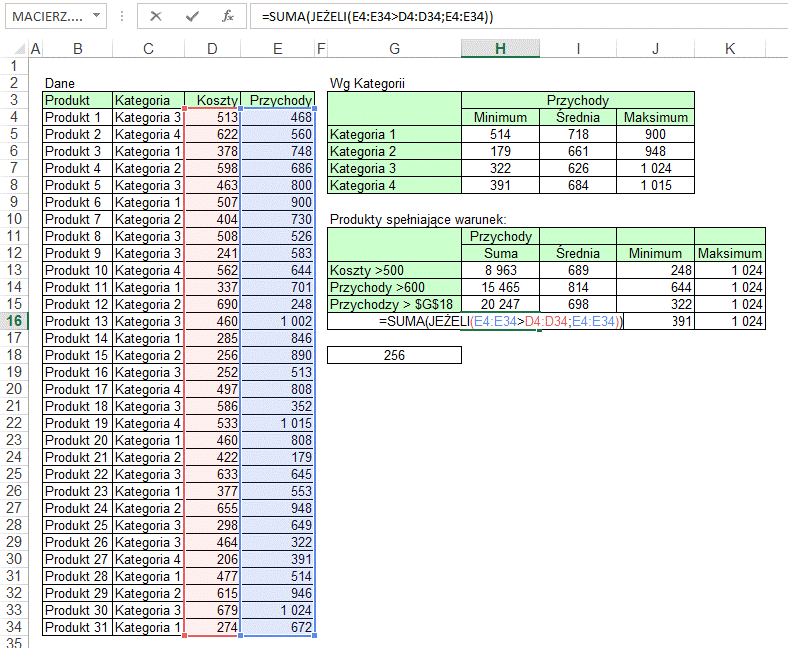
Podobnie jak wcześniej, po napisaniu funkcji na sumę, funkcje tablicowe dla średniej, minimum i maksimum utworzymy poprzez skopiowanie i zmiany w funkcji sumującej.

Przykład 4.

(Arkusz: ‘Funkcje Tablicowe 4’)

W poniższym przykładzie prezentuję funkcję tablicową, która dla rekordów spełniających warunek wylicza marżę średnią ważoną.

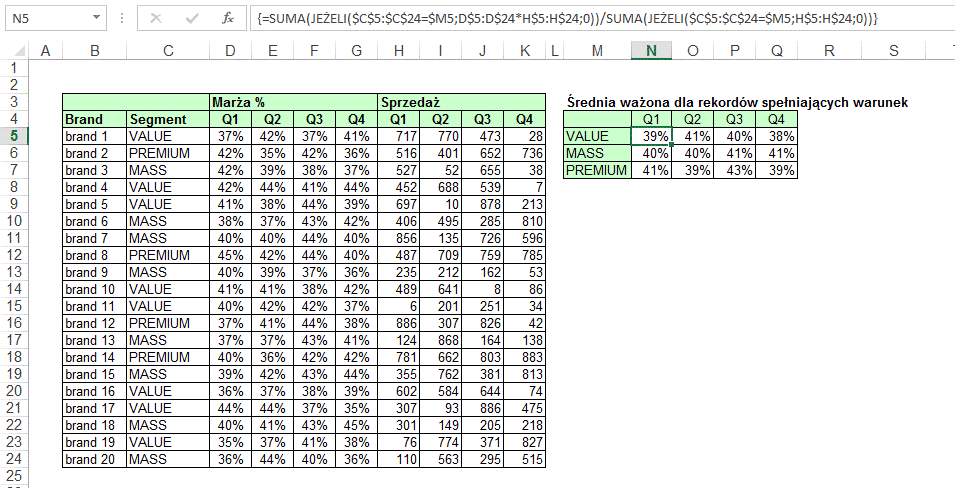
Funkcja tablicowa {=SUMA(JEŻELI($C$5:$C$24=$M5;D$5:D$24*H$5:H$24;0))/SUMA(JEŻELI($C$5:$C$24=$M5;H$5:H$24;0))} składa się z 2 elementów:

Pierwszy element SUMA(JEŻELI($C$5:$C$24=$M5;D$5:D$24*H$5:H$24;0)) dla rekordów spełniających warunek $C$5:$C$24=$M5 przemnaża marżę procentową D$5:D$24 przez sprzedaż H$5:H$24 uzyskując w ten sposób marżę kwotową dla rekordów spełniających warunek.

Drugi element to już zwykłe połączenie sumy i jeżeli, które przerabialiśmy w poprzednich przykładach. SUMA(JEŻELI($C$5:$C$24=$M5;H$5:H$24;0)) Ten element sumuje sprzedaż dla rekordów spełniających warunek.

Ostatecznie dzielimy marżę kwotową (1 element) przez sumę sprzedaży (2 element) uzyskując marżę średnią ważoną sprzedażą.

Przykład 5.

Suma pomijająca błędy

(Arkusz: ‘Suma pomijająca błędy’)

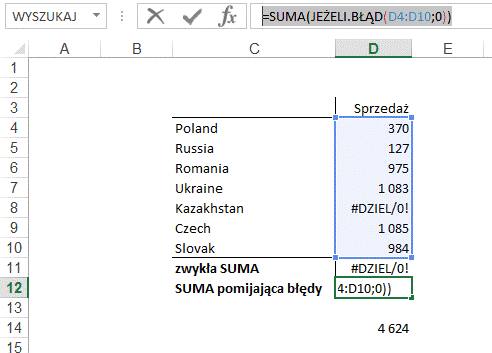
Jeżeli chcemy zsumować dane w których może wystąpić błąd możemy użyć wielu funkcji JEŻELI.BŁĄD(), w poniższym przykładzie byłaby to następująca formuła.

=JEŻELI.BŁĄD(D4;0)+JEŻELI.BŁĄD(D5;0)+JEŻELI.BŁĄD(D6;0)+JEŻELI.BŁĄD(D7;0)+JEŻELI.BŁĄD(D8;0)+JEŻELI.BŁĄD(D9;0)+JEŻELI.BŁĄD(D10;0)

Dokładnie to samo wykona poniższa formuła tablicowa.

{=SUMA(JEŻELI.BŁĄD(D4:D10;0))}

Przykład 6.

Użycie tablicy wprowadzonej

(Arkusze: ‘Użycie tablicy wprowadzonej’, ‘MIN.K MAX.K’)

Tablice wprowadzone mogą być używane zarówno w zwykłych funkcjach, jak i tablicowych.

Dość często w formułach wprowadzamy różne teksty, wartości liczbowe.

A co jeśli chcielibyśmy wprowadzić w dane miejsce funkcji nie jedną ale kilka takich elementów.

W części przypadków mogłyby pomóc funkcje Excela np. LUB() ale w wielu innych użycie tablicy wprowadzonej jest najlepszym, jeśli nie jedynym sposobem rozwiązania problemu.

W poniższym przykładzie użytkownicy wprowadzali nazwy ulic, alei i placów. Część z nich przed nazwami dodawała skróty „ul.”, „al.” lub „pl.” inni tego nie robili. Teraz trudno jest porównywać takie dane ponieważ „Mokra” to zupełnie co innego niż „ul. Mokra”.

Zaczniemy od ustalenia czy skrót występuje w danej komórce. Wycinamy przy pomocy funkcji LEWY() trzy pierwsze znaki wpisu porównujemy je z tablicą wprowadzoną {"al.";"ul.";"pl."}.

Teoretycznie powinno to wystarczyć ale dopiero po dodaniu funkcji LUB formuła będzie działać poprawnie.

Jeżeli tekst w kolumnie B zaczyna się od „ul.”, „al.” lub „pl.”, funkcja przyjmuje wartość 5, w przeciwnym razie 1.

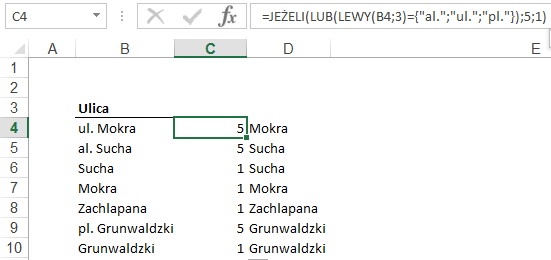
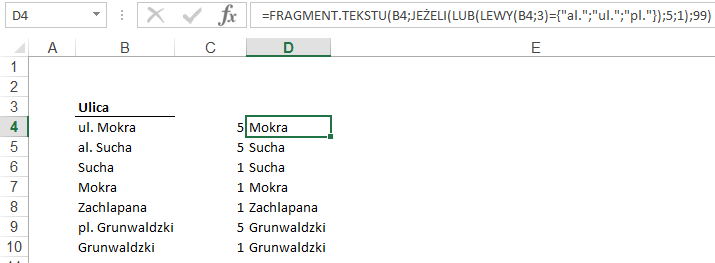
Pozostaje nam już tylko nałożenie na tą funkcję FRAGMENT.TEKSTU(), który wytnie tekst z kolumny B zaczynając od 1 lub 5 znaku.

Ilość znaków 99 została wprowadzona z zapasem, żadna ulica nie ma aż tak długiej nazwy, nadmiar nie robi problemu.

Formuła ta nie używa formuł z kolumny C, formuł tych używałem jedynie do wytłumaczenia całości w 2 krokach.

Tablica wprowadzona {"al.";"ul.";"pl."} to 3 elementowa tablica z 1 wierszem danych.

Tablica {"al."\"ul."\"pl."} to 3 elementowa tablica z 1 kolumną danych.

Średnikiem oznaczamy kolejny element w wierszu, znakiem \ kolejny wiersz.

Tablica {„a”;”b”\”c”;”d”} ,ma 2 wiersze i dwie kolumny, czyli 4 elementy.

W kolejnym przykładzie zaczynającym się od kolumny F przemnażamy przez siebie i sumujemy 2 zbiory liczb. 3 liczby parzyste i 3 nieparzyste.

Możemy użyć do tego funkcji tablicowej {=SUMA(G3:I3*G4:I4)}

Lub też skorzystać z tablicy wprowadzonej i zwykłej sumy.

=SUMA(G3:I3*{1\3\5})

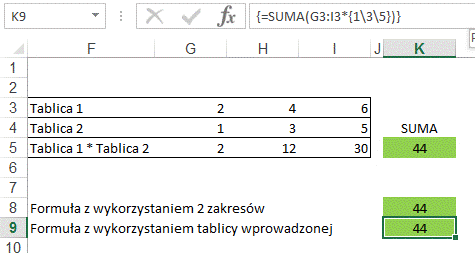
Tablica wprowadzona musi być pionowa, tak jak w macierzach będziemy mnożyć tablicę poziomą przez pionową.

W arkuszu ‘MIN.K MAX.K’ są kolejne przykłady użycia tablicy wprowadzonej.

Funkcje MIN.K i MAX.K zostały omówione w lekcji ‘Funkcje dla Ekspertów’.

Funkcja =SUMA(MIN.K(C3:C12;{1;2;3})) będzie sumować 3 najmniejsze wartości z zakresu C3:C12

Funkcja =SUMA(MAX.K(C3:C12;{1;2;3})) będzie sumować 3 największe wartości z zakresu C3:C12

Nie są to funkcje tablicowe i ich wprowadzania nie należy kończyć Ctrl+Shit+Enter

W tych przykładach użyto tablice wprowadzone zawierające 3 elementy w 1 wierszu, równie dobrze moglibyśmy użyć tablicy z 1 kolumną i 3 elementami, ale w znacznie większej ilości przypadków to czy tablica jest ‘pionowa’ czy ‘pozioma’ nie będzie obojętne dla wyniku.

UWAGA

Niestety podczas używania tablic wprowadzonych należy zachować dużą ostrożność ponieważ Excel nie zawsze zachowuje się logicznie i konsekwentnie.

Podobnie przy użyciu funkcji LUB() i ORAZ() w funkcjach tablicowych wymagana jest duża ostrożność ponieważ Excel nie zawsze jest konsekwentny.

Przykład 7.

Ile unikatów

(Arkusz: ‘Ile unikatów’)

Ilość unikatów to jedna z funkcji, której zdecydowanie brakuje w standardowych funkcjach Excela.

Możemy ją przygotować i dodać do funkcji samodzielnie przy użyciu VBA, ale znacznie prostsza jest funkcja tablicowa.

Zacznijmy od kilku prostych formuł.

Funkcja LICZ.JEŻELI zliczy ile razy występuje na liście każdy z jej elementów.

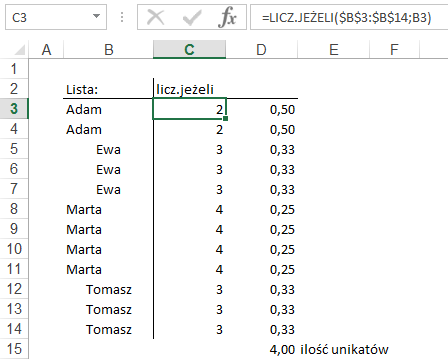
Jeżeli podzielimy 1 przez ilość występowania danego elementu to suma tych ułamków dla wszystkich linii które zawierają dany element zawsze będzie wynosić 1.

Np. „Adam” występuje 2 razy ½+½=1, „Ewa” występuje 3 razy ⅓+⅓+⅓=1.

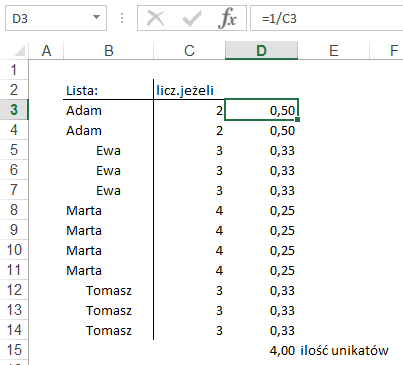
Na koniec sumujemy te dane w komórce D15.

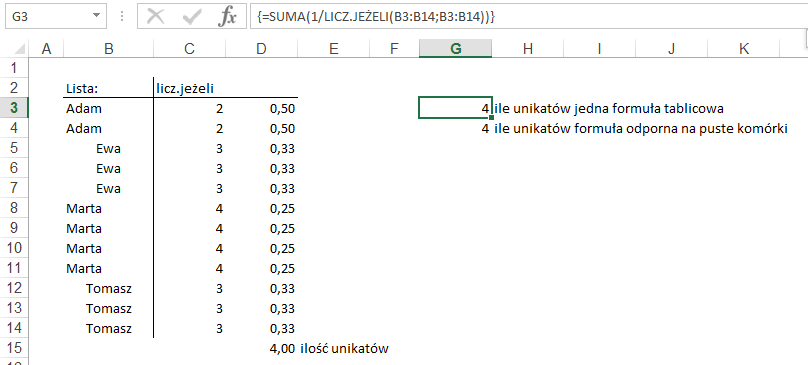
Teraz zrobimy to samo w jednej komórce używając funkcji tablicowej.

Poniższa formuła liczy ilość wystąpień, każdorazowo oblicza jego odwrotność dzieląc jedynkę przez tą wartość, ostatecznie sumując wszystkie wyniki.

Przedstawiony tu sposób obliczania i formuła tablicowa nie będzie działać poprawnie jeśli w zakresie znajdzie się pusta komórka. Niezależnie od ilości wystąpień pustych komórek w zakresie, funkcja LICZ.JEŻELI zawsze przyjmuje wynik 0 dla pustych komórek.

Aby poradzić sobie z tym problemem wystarczy dodać funkcję JEŻELI, która dla zer nie będzie dzielić przez nie jedynki ale przyjmie wartość 0.

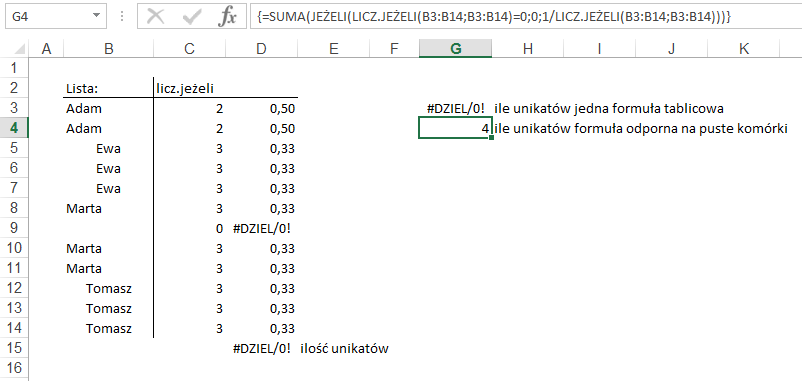
Pusta komórka nie jest unikalną wartością w zakresie. Unikalnych pozycji na liście jest nadal 4.

Przykład 8.

Wartość najbliższa

(Arkusz: ‘Wartość najbliższa)

W wielu firmach przygotowuje się różnego typu prognozy lub korzysta z prognoz przygotowanych przez ekspertów.

Czasami dział estymacji liczy nawet kilkadziesiąt osób.

Przy takich nakładach warto byłoby w prosty sposób ustalać czyja prognoza była najbliższa rzeczywistych wyników.

W poniższym przykładzie zebrano prognozy Ekspertów którzy szacowali jaki będzie kurs €.

Ponieważ nadszedł już dzień który był prognozowany możemy i wiemy że ostatecznie wyniósł on 4,15zł obliczymy kto był najbliżej.

Zaczniemy od wyliczeń w tabeli. W kolumnie E odejmujemy od kursu prognozowanego kurs osiągnięty. Aby wszystkie wartości (odległości od celu) były dodatnie i dzięki temu porównywalne na te obliczenia nałożyliśmy funkcję MODUŁ.LICZBY, która z liczb ujemnych robi dodatnie a dodatnich nie zmienia, czyli innymi słowy podaje odległość liczby od zera.

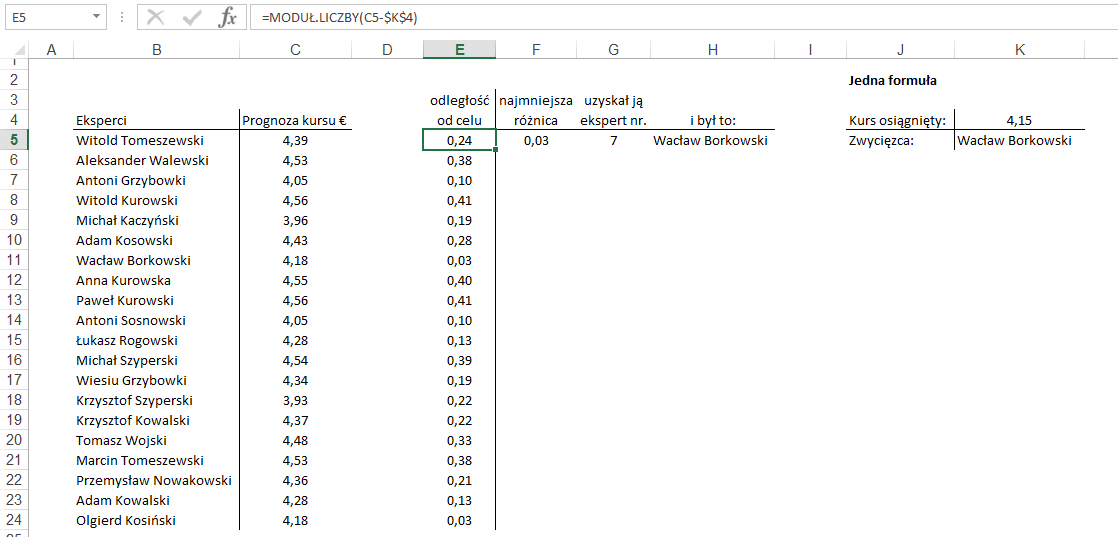
Następnie wyznaczamy który wynik był najmniejszy używając funkcji MIN – komórka F5.

W komórce G5 używając funkcji PODAJ.POZYCJĘ ustalamy który z ekspertów uzyskał ten wynik.

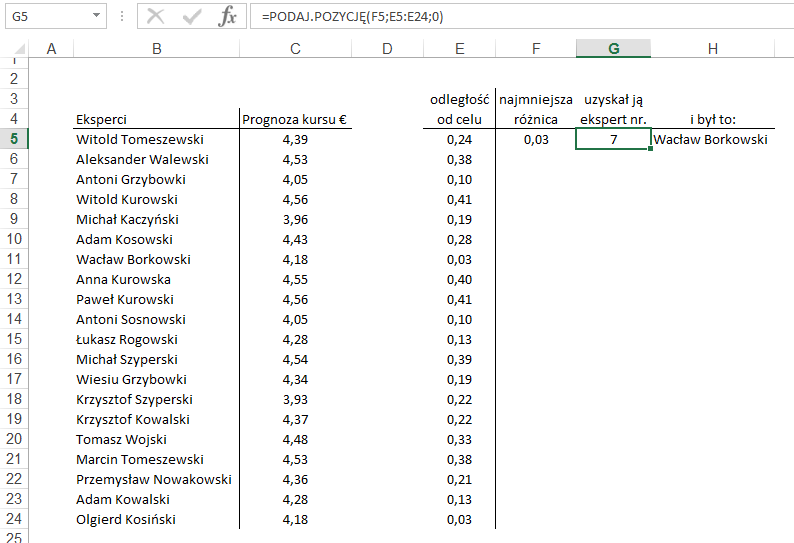
By wreszcie w komórce H5, znaleźć jego nazwisko używając funkcji INDEKS.

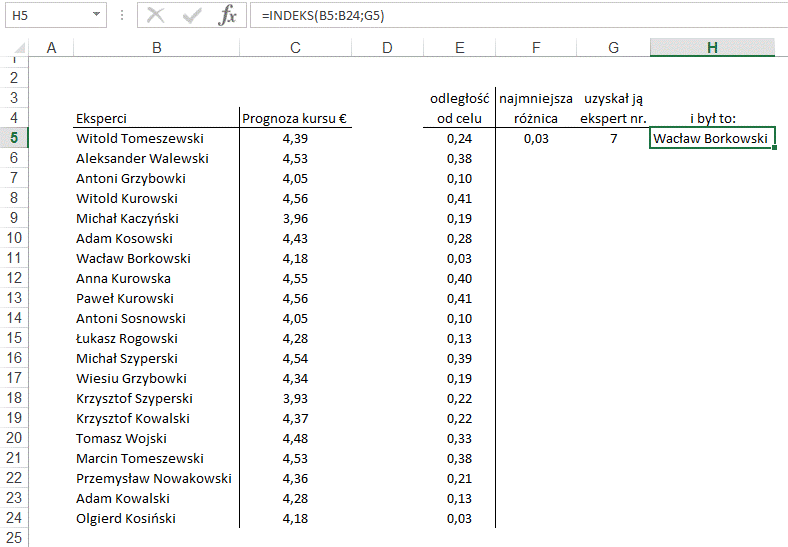
Teraz to samo zrobimy w jednej komórce używając funkcji tablicowej.

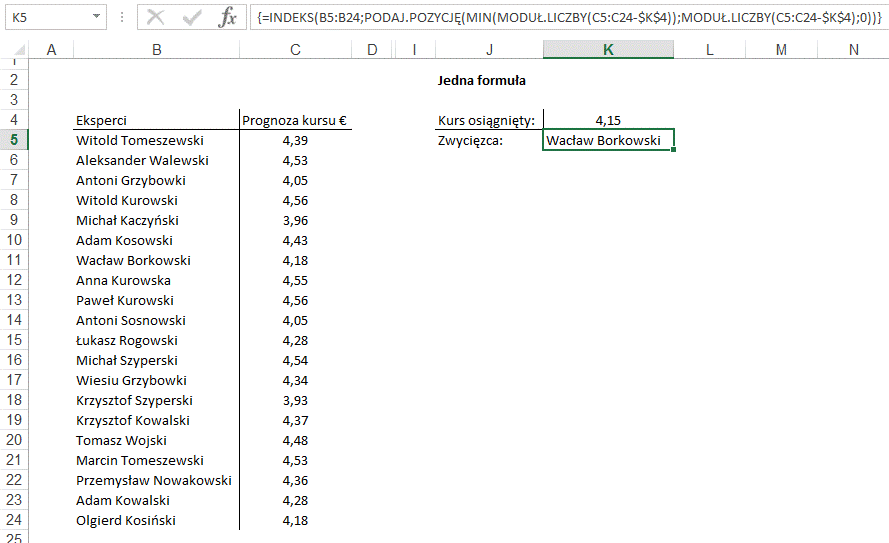
Funkcję taką możemy uzyskać „sklejając” i modyfikując wcześniej używane formuły.

{=INDEKS(B5:B24;PODAJ.POZYCJĘ(MIN(MODUŁ.LICZBY(C5:C24-$K$4));MODUŁ.LICZBY(C5:C24-$K$4);0))}

Przykład 9.

Dana występuje x razy

(Arkusz: ‘Dana występuje x razy’)

Gdybyśmy chcieli sprawdzić czy dana występuje w tabeli możemy posłużyć się złożeniem funkcji JEŻELI i SUMA.

Dzięki takiej funkcji wiemy od razu nie tylko czy występuje ale też od razu ile razy.

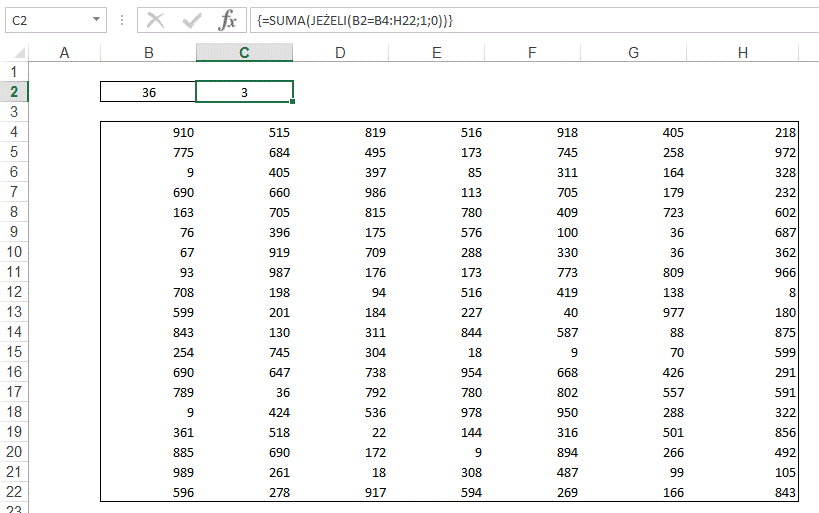
Taka formuła jest też odporna na puste komórki i także ich ilość będzie poprawnie zliczać.

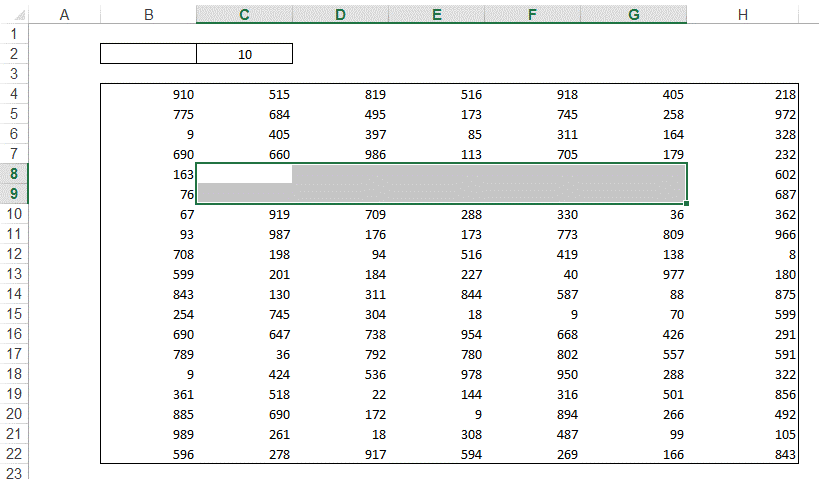
Gdybyśmy jednak potrzebowali informacji „Występuje”, „Nie występuje”, wystarczy nałożyć na tą funkcję jeszcze jedno JEŻELI.

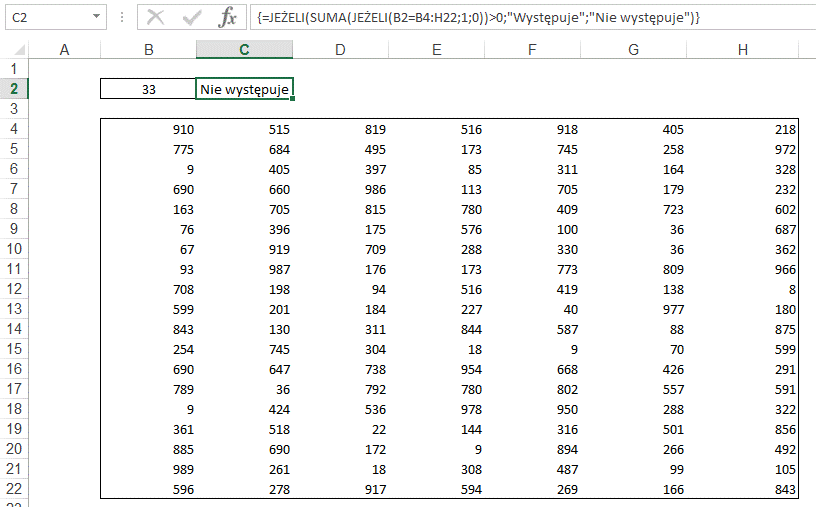
A gdybyśmy chcieli mieć informację „Nie występuje” lub np. „Występuje 3 razy” będziemy dalej rozwijać naszą formułę.

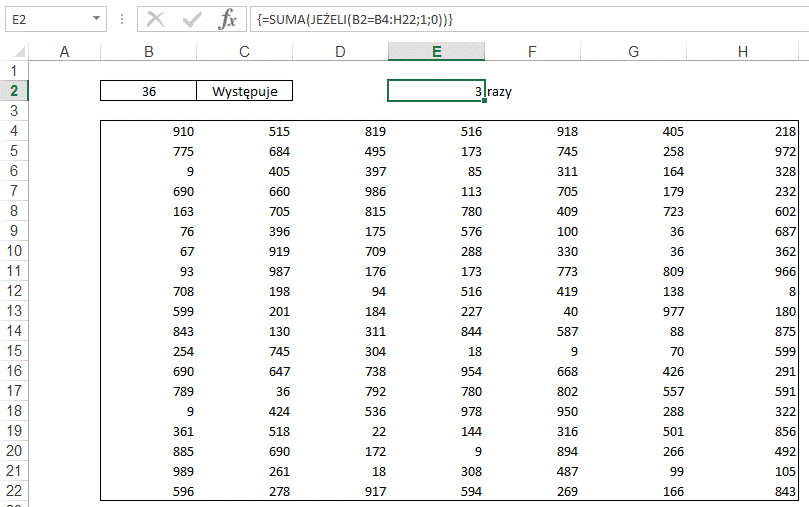
Zacznijmy od znanej nam już formuły zliczającej.

Oraz drugiej, która będzie dodać „raz” lub „razy”.

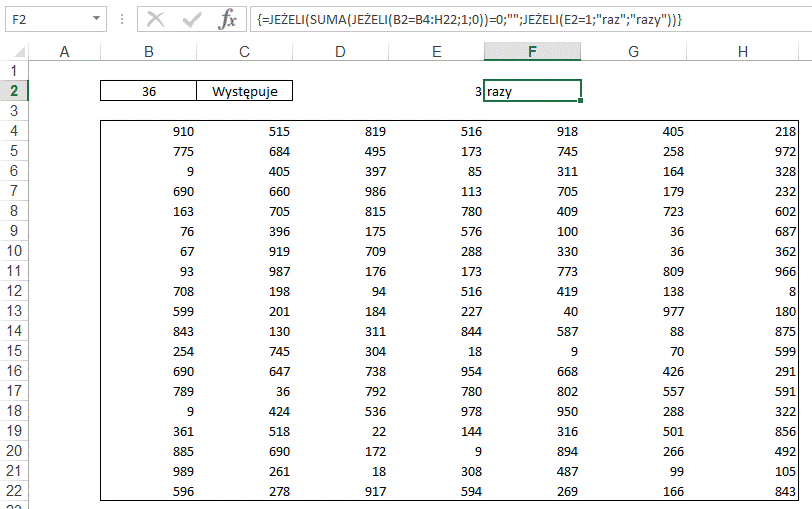
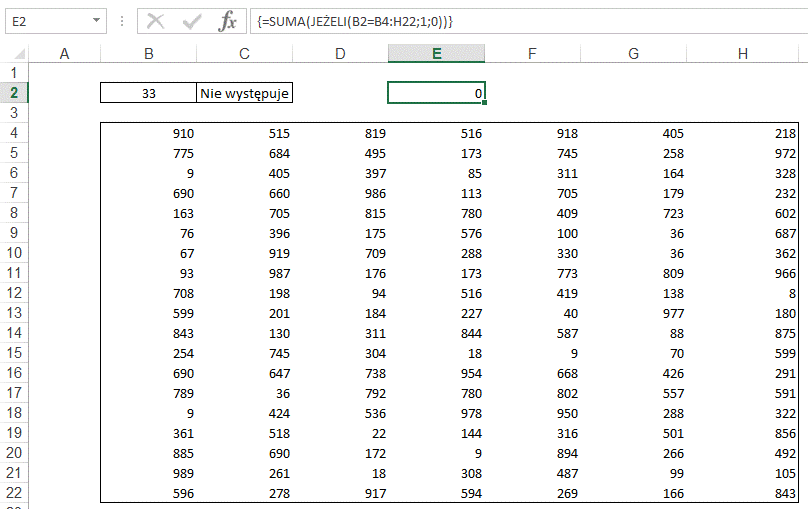
Jak można zobaczyć powyżej w przypadku gdy dana nie występuje na ten moment nic nie jest wpisywana, a funkcja nie działa poprawnie i pokazuje tylko zero.

W ostatnim kroku połączymy te funkcje i dodamy obsługę „Nie występuje”.

Formuła przyjmie postać:

{=JEŻELI(SUMA(JEŻELI(B2=B4:H22;1;0))>0;"Występuje";"Nie występuje")&" "&JEŻELI(SUMA(JEŻELI(B2=B4:H22;1;0))=0;"";JEŻELI(SUMA(JEŻELI(B2=B4:H22;1;0))=1;SUMA(JEŻELI(B2=B4:H22;1;0))&" "&"raz";SUMA(JEŻELI(B2=B4:H22;1;0))&" "&"razy"))}

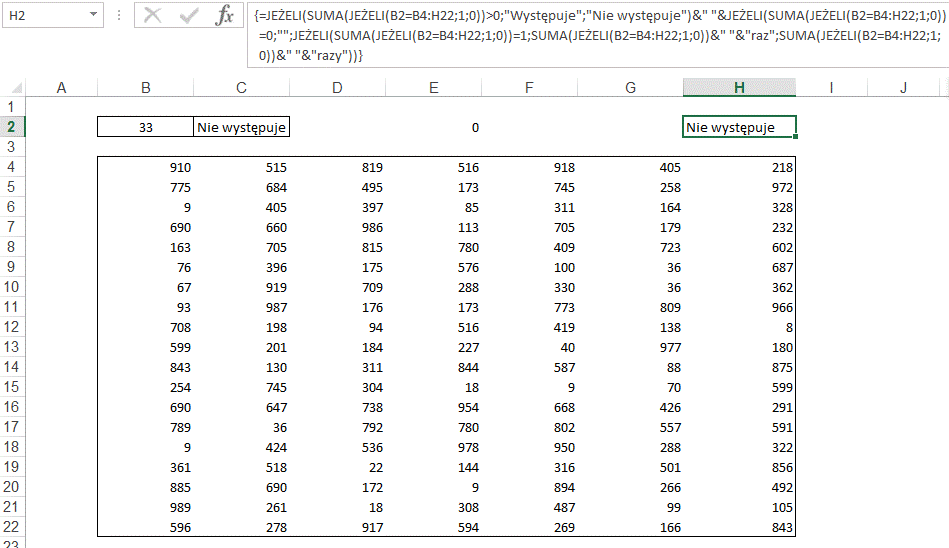
Pierwsza jej cześć wprowadza tylko słowa „Występuje” lub „Nie występuje”.

{=JEŻELI(SUMA(JEŻELI(B2=B4:H22;1;0))>0;"Występuje";"Nie występuje")

Dodajemy spacje

…&" "&…

Jeżeli „Nie występuje” nic "" więcej nie dodajemy.

…JEŻELI(SUMA(JEŻELI(B2=B4:H22;1;0))=0;"";…

A gdy występuje obliczamy liczbę powtórzeń do której doklejamy spację oraz słowo „raz” lub „razy”.

…JEŻELI(SUMA(JEŻELI(B2=B4:H22;1;0))=1;SUMA(JEŻELI(B2=B4:H22;1;0))&" "&"raz";SUMA(JEŻELI(B2=B4:H22;1;0))&" "&"razy"))}

Korzystając z ostatecznej wersji tej formuły chciałbym zaprezentować narzędzie: ‘Szacuj formułę’, dzięki któremu możemy zrozumieć skomplikowane formuły.

Często także te napisane przez nas samych już jakiś czas temu.

Narzędzie to znajdziemy na karcie ‘FORMUŁY’.

Uruchamiamy je stojąc w komórce H2, gdzie znajduje się skomplikowana formuła.

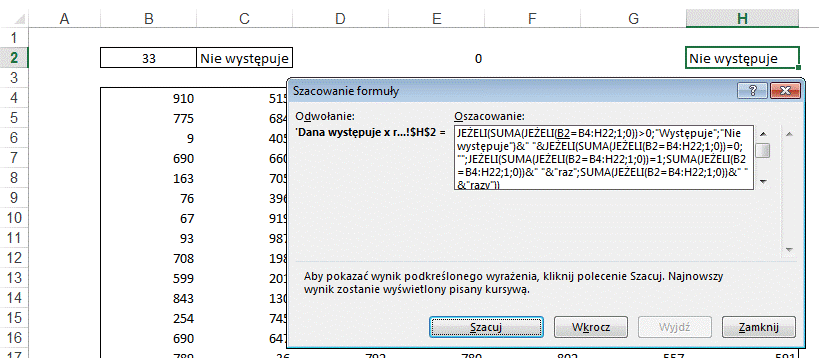
Klikamy przycisk ‘Szacuj’ i obserwujemy zmiany zachodzące w formule. To która z jej części zostanie przeliczona jest podkreślane. Powyżej widać że zmiana będzie dotyczyć komórki B2.

Po kliknięcie ‘Szacuj’ B2 zastępowane jest wartością 33 która znajduje się tej komórce. Oraz podkreślona zostanie kolejna część formuły, porównanie 33 z komórkami w zakresie B4:H22.

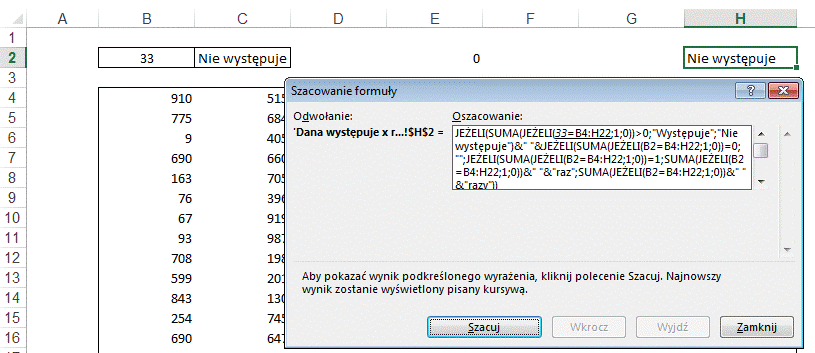
Wynikiem tych porównań jest XXX wyników ‘PRAWDA’ lub ‘FAŁSZ’. Jest ich tyle ile komórek w zakresie B4:H22.

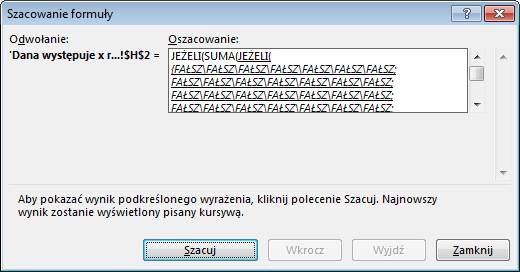
Następnie ‘PRAWDA’ i ‘FAŁSZ’ zostają zastąpione 1 i 0. W tym przypadku są same zera.

Podkreślona jest funkcja SUMA, która zsumuje te wszystkie cyfry.

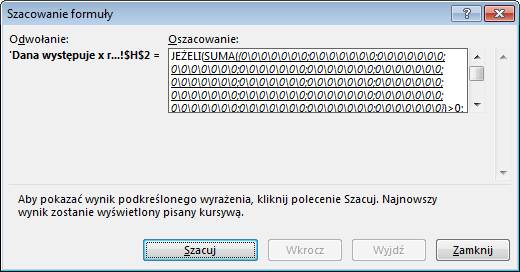
W kolejnych krokach nastąpi porównanie i przejście do właściwej części funkcji JEŻELI.

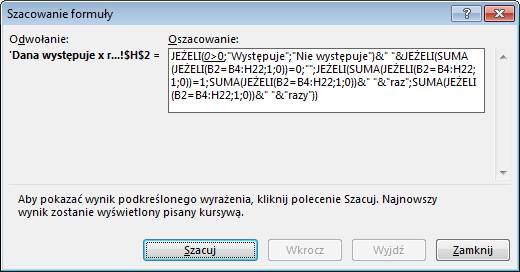
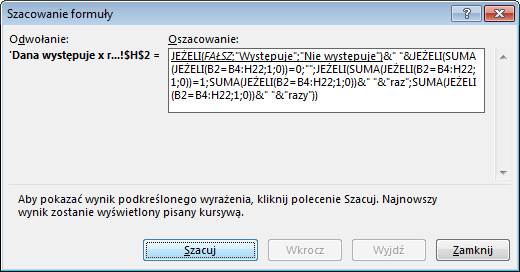
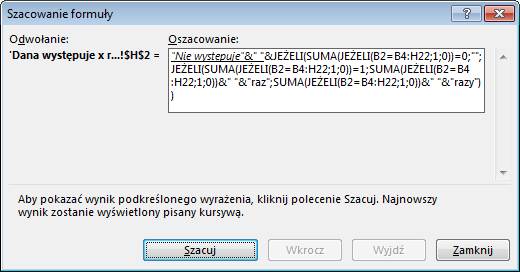
Itd.

Ciekawszym (i dłuższym) szacowaniem tej funkcji jest przypadek gdy szukana wartość występuje w tabeli. Zachęcam do jego prześledzenia.

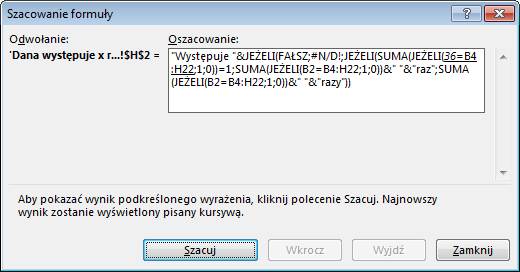
W takim przypadku w jednym z kroków może nas zdziwić fakt że w funkcji JEŻELI, gdy już wiadomo że mamy do czynienia z FAŁSZEM wartość dla PRAWDY zastępowana jest przez #N/D!, nie będzie ona używana i w ten sposób jest to oznaczane przez Excela, #N/D! nie będzie stanowić problemu przy rozwiązaniu tej formuły.

Nie można używać wielokomórkowych funkcji i formuł tablicowych w zdefiniowanych tabelach Excela opisanych w lekcji ‘Tabela’.

Funkcje tablicowe dają bardzo dużo możliwości, powyżej przedstawiłem tylko krótki wstęp do nich.

Jeszcze jeden przykład wykorzystania funkcji tablicowych znajduje się w lekcji Tabela Danych.