Solver

Przykłady opisane w tej lekcji dostępne są w arkuszu Excela: Solver.xlsx tylko ich samodzielne przerobienie daje gwarancję zapamiętania tej lekcji

Przykłady dla wszystkich lekcji szkolenia Excel 2013: ExcelSzkolenie.pl Cwiczenia Excel 2013.zip

Ta lekcja może być obejrzana lub przeczytana poniżej.

Film wygląda najlepiej jeśli będzie odtwarzany w rozdzielczości 720p HD, rozdzielczość można zmienić dopiero po uruchomieniu filmu klikając na ikonie trybika która pojawi się w prawym dolnym rogu poniższego ekranu. Po kilku sekundach od zmiany obraz wyostrzy się.

W mojej praktyce biznesowej nie zdarzyło mi się używać Solvera ani poznać nikogo kto używałby go do rozwiązywania realnych problemów korporacji.

Wynika to z faktu że dla większości procesów biznesowych nie da się określić wyników za pomocą dokładnych funkcji matematycznych, takie podejście zawsze wymaga przyjęcia założeń i to głównie od tego jakie założenia przyjmiemy będzie zależeć ostateczny wynik.

Myślę że narzędzie to może przydać się przy optymalizacji procesów produkcyjnych lub logistycznych, choć przyznaję, że osobiście w praktyce takimi się nie zajmowałem.

Bardzo często znajomość Solvera wymagana jest przez ambitnych nauczycieli akademickich i głównie do studentów takich nauczycieli skierowana jest ta lekcja.

Aby mieć możliwość używania Solvera należy najpierw zainstalować ten dodatek Excela.

Klikamy Menu ‘PLIK’ " ‘Opcje’ " karta ‘Dodatki’ " przycisk ‘Przejdź…’.

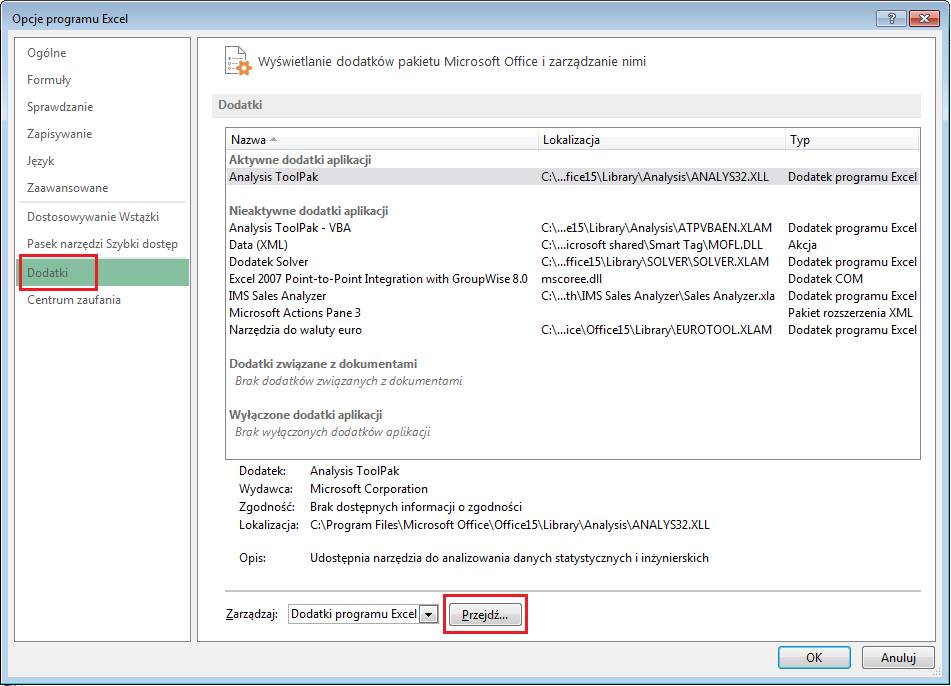
W okienku, które zostanie wyświetlone wybieramy ‘Dodatek Solver’ i klikamy ‘OK’.

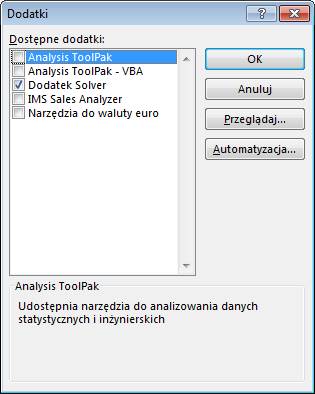
Od tego momentu na karcie ‘DANE’ w grupie ‘Analiza’ znajdziemy dodatek ‘Solver’

Przykład 1.

(Arkusz: ‘Solver 1’)

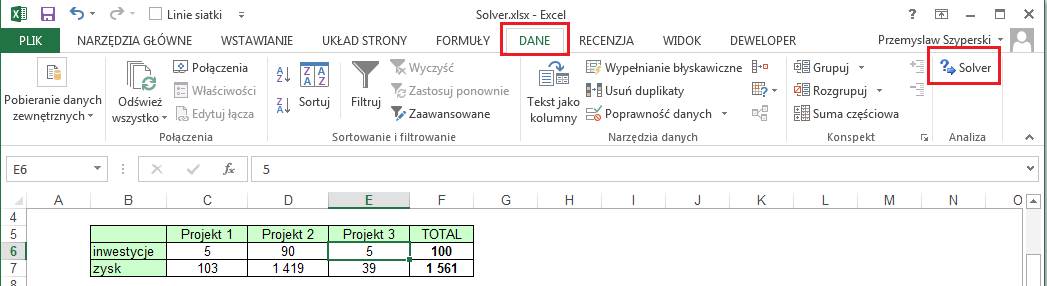
W poniższym przykładzie mamy do dyspozycji budżet w wysokości 100mln USD i trzy projekty, które możemy dofinansować.

Każdy projekt może zostać sfinansowany w dowolnym zakresie, ale niewłaściwie dobrana wielkość inwestycji może powodować straty, które mogą nawet znacznie przekroczyć samą inwestycję.

Najbardziej prawdopodobny zysk lub strata jaką każdy z tych projektów przyniesie znajduje się w linii 7.

Projekty już się toczą i przy braku dodatkowego finansowania (inwestycje 0) nie są zamykane ale z reguły przynosić będą straty.

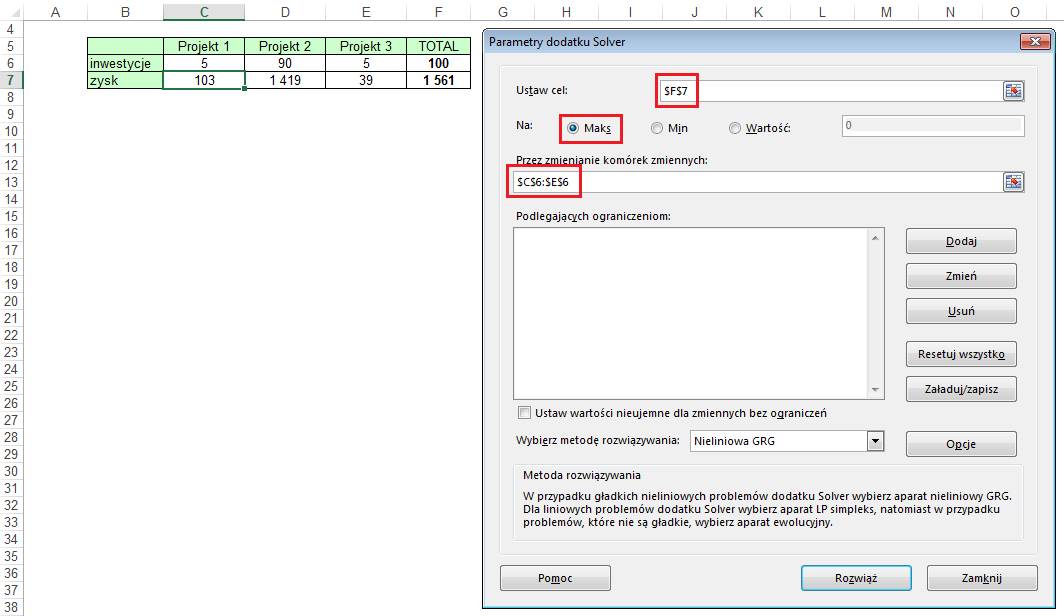
Po uruchomieniu narzędzia Solver wyświetlone zostanie okno ‘Parametry dodatku Solver’ pokazane na poniższym rysunku.

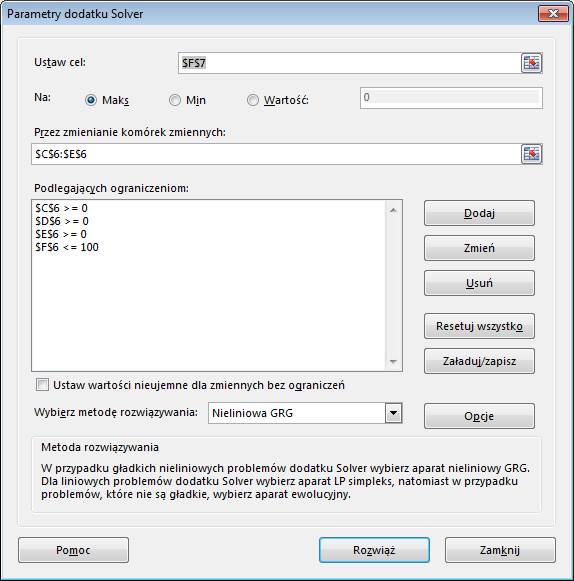
Komórka celu to suma zysku z wszystkich projektów (F7) i co jest oczywiste chcemy ją maksymalizować.

Komórki zmienne to wysokości inwestycji jakie możemy ponieść, czyli komórki od C6 do E6.

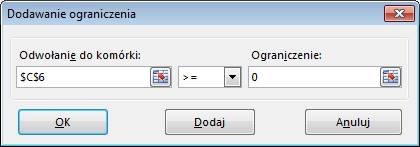
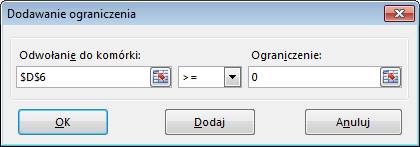
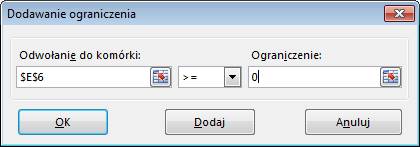
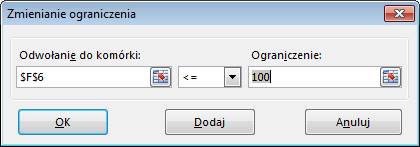
Warunki ograniczające: żadna z inwestycji nie może być ujemna i budżet jaki mamy do wydania (F6) jest mniejszy bądź równy 100.

Warunki dodajemy poprzez kliknięcie przycisku dodaj i wprowadzeniu każdego warunku osobno w oknie przedstawionym poniżej, po wprowadzeniu każdego z warunków klikamy przycisk ‘Dodaj’.

Po wprowadzeniu wszystkich warunków klikamy polecenie ‘Rozwiąż’.

Zostaje wyświetlone okno ‘Solver – Wyniki’, które pozwala nam wybrać czy chcemy zachować rozwiązanie czy też powrócić do oryginalnych cyfr.

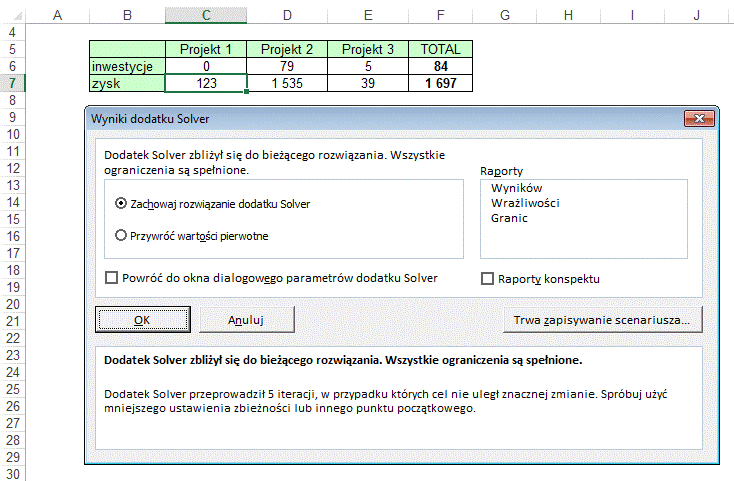
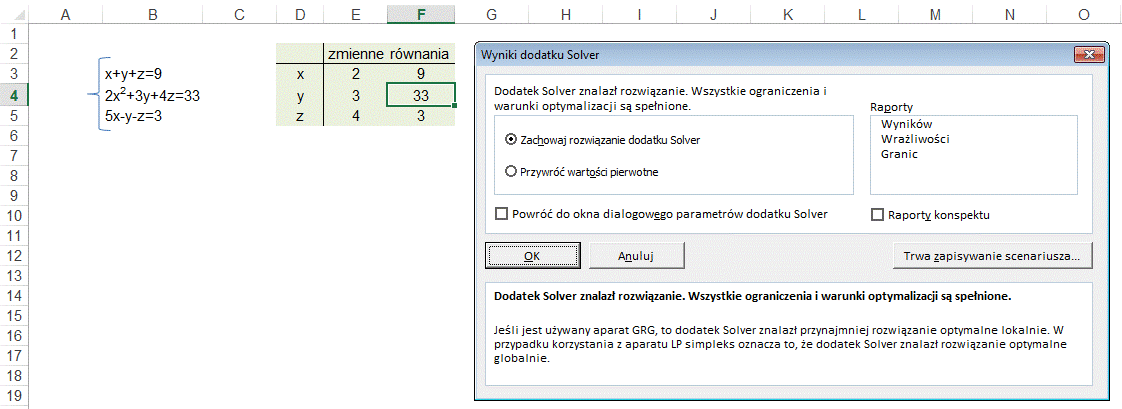
Wybieramy opcję ‘Przechowaj rozwiązanie’ i klikamy OK.

Jak widać ostateczne rozwiązanie nie wykorzystuje całości dostępnego budżetu.

Dlatego też bardzo ważna jest precyzja podczas dodawania warunków, gdybyśmy zamiast <=100 wybrali tylko =100, wynik byłby niepoprawny.

Przykład 2.

(Arkusz: ‘Solver 2’)

Solver dobrze sobie radzi z rozwiązywaniem równań dla wielu zmiennych.

W tym przykładzie rozwiążemy układ 3 równań z 3 niewiadomymi.

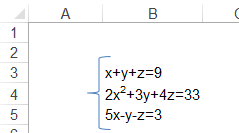
Przygotowujemy miejsce na zmienne, a formuły zapisujemy tak aby korzystały z komórek w których zmienne te pojawią się.

Liczby po drugiej stronie równań wprowadzimy w Solverze.

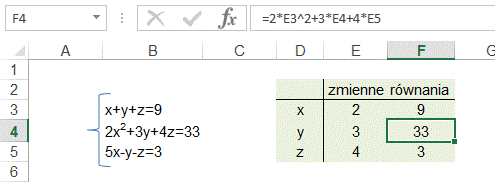
W oknie ‘Parametry dodatku Solver’ wprowadzamy zakres gdzie mają się pojawić obliczone zmienne, czyli E3:E5.

Oraz ustalamy ograniczenia, każda z formuł w komórkach F3:F5 musi równać się liczbie która jest po drugiej stronie równania.

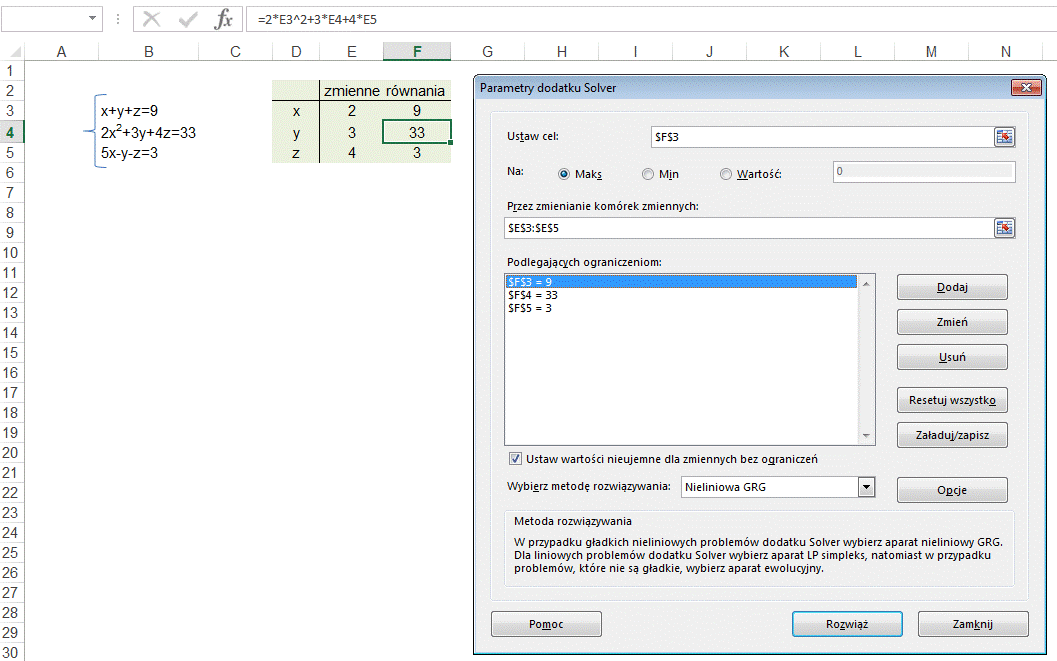
Solver znajduje poprawne rozwiązanie x=2, y=3, z=4.

Nie każdy układ będzie miał rozwiązanie, może ich także być nieskończenie wiele.

Możemy myśleć o narzędziu Solver jako o bardziej rozbudowanej opcji polecenia ‘Szukaj Wyniku’ opisanej w lekcji o takim tytule.

W przykładzie opisanym w lekcji ‘Szukaj Wyniku’ mogliśmy sami dojść do końcowego wyniku metodą prób i błędów, a polecenie ‘Szukaj Wyniku’ pozwoliło nam jedynie przyspieszyć ten proces i wyliczyć bardzo dokładny wynik.
W przypadku powyższych zadań znalezienie wyniku bez użycia Solvera wymagało by znajomości metod rozwiązywania układów równań kwadratowych dla wielu zmiennych bądź godzin spędzonych na rozwiązanie metodą prób i błędów.

W plikach ćwiczeń do tego szkolenia znajdziesz plik SOLVSAMP.xls przygotowany przez firmę Microsoft i rozprowadzany przez nią nieodpłatnie w celach szkoleniowych.

Zawiera on wiele przykładów zadań dla Solvera, wraz z ich szczegółowym opisem w języku polskim. Osobom zainteresowanym tym zagadnieniem zdecydowanie polecam je przerobić.